题目内容
【题目】（本题满分14分）如图，在正方形ABCD中，AB=5.点E为BC边上一点（不与点B重合），点F为CD边上一点，线段AE、BF相交于点O,其中AE=BF.
(1)求证：AE⊥BF；
(2)若OA-OB=1，求OA的长及四边形OECF的面积；
(3)连接OD,若△AOD是以AD为腰的等腰三角形，求AE的长.
【答案】（1）证△ABE≌△BCF（2）OA=4，6
（3）
【解析】在△ABE和△BCF中
∵AB=BC,AE=BF
∴△ABE≌△BCF(HL),
∴∠BAE=∠CBF.
∵∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴AE⊥BF.
设OA=x,则OB=x-1.
由勾股定理得
解之得
，
（舍去）
.
,
,
,
.
,
,
,
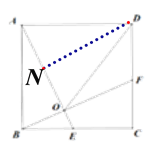
（3）由题意知AD=OD.作DN⊥AE于点N.
在△ABO和△DAN中
∵∠AOB=∠AND, ∠DAN=∠ABO,AD=AB
∴△ABO≌△DAN（AAS）
∴AN=ON=OB
设AN=ON=OB=x，则OA=2x.
由勾股定理得
解之得
.
∵△ABO∽△AEB
, 
，
.
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
