题目内容
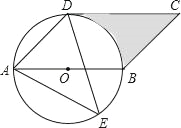
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的位置关系,并说明理由.
(2)若BC=2.求阴影部分的面积.(结果保留π的形式)
【答案】(1)CD与⊙O的位置关系是相切.(2)3﹣![]() π.
π.
【解析】
(1)接BD、OD,求出∠ABD=∠AED=45°,根据DC∥AB,推出∠CDB=45°,求出∠ODC=90°,根据切线的判定推出即可;
(2)求出∠AOD=∠BOD=90°,求出AO、OD,分别求出△AOD、扇形BOD、平行四边形ABCD的面积,相减即可求出答案.
(1)解:CD与⊙O的位置关系是相切.
理由是:连接BD、OD,
∵∠AED=45°,
∴∠ABD=∠AED=45°,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=45°,
∵OD=OB,
∴∠ODB=∠OBD=45°,
∴∠ODC=45°+45°=90°,
∵OD为半径,
∴CD与⊙O的位置关系是相切;
(2)解:∵AB∥CD,∠ODC=90°,
∴∠BOD=90°=∠AOD,
∵四边形ABCD是平行四边形,
∴AD=BC=2,
在△AOD中,由勾股定理得:2AO2=22,
AO=OD=OB=![]() ,
,
∵S△AOD=![]() OA×OD=
OA×OD=![]() ,
,
S扇形BOD=![]()
S平行四边形ABCD=AB×DO=![]() ,
,
∴阴影部分的面积是:![]() .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目