��Ŀ����
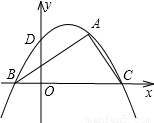
��֪��Rt��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����A=90�㣬��B��C����x���ϣ��ҵ�A��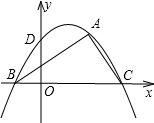 ����Ϊ��2��
������2��
������ABC=30�㣬��������y=ax2+bx+cǡ�ù�A��B��C���㣬����y�ύ�ڵ�D��
��1�����B��C�������������y=ax2+bx+c�Ľ���ʽ��
��2������E��������y=ax2+bx+c�Գ�����һ���㣬��ȷ������E�ںδ�ʱ����AEC���ܳ���С����С�Ƕ��٣�
��3������PΪ�������ڵ�һ����ͼ���ϵĶ��㣬��ȷ������P�ںδ�ʱ���ı���PDBC�������������������
 ������2��
������2��| 3 |
��1�����B��C�������������y=ax2+bx+c�Ľ���ʽ��
��2������E��������y=ax2+bx+c�Գ�����һ���㣬��ȷ������E�ںδ�ʱ����AEC���ܳ���С����С�Ƕ��٣�
��3������PΪ�������ڵ�һ����ͼ���ϵĶ��㣬��ȷ������P�ںδ�ʱ���ı���PDBC�������������������
��������1�����ȹ���A��AF��x���ڵ�F���ɵ�A������Ϊ��2��
������ABC=30�㣬����ֱ�������ε����ʣ�������õ�B��C�����꣬Ȼ�����ô���ϵ����������ö��κ����Ľ���ʽ��
��2���ɣ�1��������������ߵĶԳ��ᣬ���ɵ�B��C����ֱ��x=1�Գƣ����AEC���ܳ�����Сֵ����Ϊ��AE+EC+AC����Сֵ���ɶԳ���֪��AE+EC����СֵΪAB�ij���������E�˶���AB�������߶Գ���x=1�Ľ��㴦ʱ����AEC���ܳ���С���̶�����ô𰸣�
��3���������ӽ�PO�����P������Ϊ��t��-
t2+
t+
��������P�ֱ��� x�ᣬy�������ߣ�����ֱ�ΪN��G����S�ı���PDBC=S��POC+S��POD+S��BOD��������ô𰸣�
| 3 |
��2���ɣ�1��������������ߵĶԳ��ᣬ���ɵ�B��C����ֱ��x=1�Գƣ����AEC���ܳ�����Сֵ����Ϊ��AE+EC+AC����Сֵ���ɶԳ���֪��AE+EC����СֵΪAB�ij���������E�˶���AB�������߶Գ���x=1�Ľ��㴦ʱ����AEC���ܳ���С���̶�����ô𰸣�
��3���������ӽ�PO�����P������Ϊ��t��-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
����⣺��1������A��AF��x���ڵ�F����Rt��AFB�У�
�ߡ�ABC=30�㣬��A������Ϊ��2��
����
��OF=2��AF=
����ACF=60�㣬
��BF=
=3��
��OB=BF-OF=3-2=1��
���B�ĵ��Ϊ��-1��0����
��Rt��AFC�У��ɡ�ACF=60�㣬
��FC=
=1��
���C��������3��0����
��A��B��C��������ֱ����y=ax2+bx+c�ã�
��
��ã�
��
������ߵĽ���ʽΪ��y=-
x2+
x+
����4�֣�
��2����y=-
x2+
x+
=-
��x-1��2+
��
�������ߵĶԳ���Ϊx=1��
���B��C����ֱ��x=1�Գƣ�
���AEC���ܳ�����Сֵ����Ϊ��AE+EC+AC����Сֵ��
�ɶԳ���֪��AE+EC����СֵΪAB�ij���������E�˶���AB�������߶Գ���x=1�Ľ��㴦ʱ����AEC���ܳ���С��
��B��-1��0����A��2��
���ɵ�AB����ֱ�ߵĽ���ʽΪ��y=
x+
������7�֣�
��x=1ʱ��y=
��
�ʵ�E������Ϊ��1��
����
��ʱ����AEC���ܳ���С����СֵΪAB+AC=2
+2����8�֣�
��3�����ӽ�PO�����P������Ϊ��t��-
t2+
t+
������O��t��3��
����P�ֱ��� x�ᣬy�������ߣ�����ֱ�ΪN��G��
�ɣ�1��֪����D������Ϊ��0��
������9�֣�
��S�ı���PDBC=S��POC+S��POD+S��BOD
=
��OC��PN+
��OD��PG+
��OB��OD
=
��3����-
t2+
t+
��+
��
��t+
��1��
=-
(t-
)2+
����11�֣�
�ʵ�t=
ʱ���ı���PDBC��������������Ϊ
��
��ʱ��P������Ϊ��
��
��������12�֣�
�ߡ�ABC=30�㣬��A������Ϊ��2��
| 3 |
��OF=2��AF=
| 3 |
��BF=
| AF |
| tan30�� |
��OB=BF-OF=3-2=1��
���B�ĵ��Ϊ��-1��0����
��Rt��AFC�У��ɡ�ACF=60�㣬
��FC=
| AF |
| tan60�� |
���C��������3��0����

��A��B��C��������ֱ����y=ax2+bx+c�ã�
|
��ã�
|
������ߵĽ���ʽΪ��y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
��2����y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
=-
| ||
| 3 |
4
| ||
| 3 |
�������ߵĶԳ���Ϊx=1��
���B��C����ֱ��x=1�Գƣ�
���AEC���ܳ�����Сֵ����Ϊ��AE+EC+AC����Сֵ��
�ɶԳ���֪��AE+EC����СֵΪAB�ij���������E�˶���AB�������߶Գ���x=1�Ľ��㴦ʱ����AEC���ܳ���С��
��B��-1��0����A��2��
| 3 |
| ||
| 3 |
| ||
| 3 |
��x=1ʱ��y=
2
| ||
| 3 |
�ʵ�E������Ϊ��1��
2
| ||
| 3 |
��ʱ����AEC���ܳ���С����СֵΪAB+AC=2
| 3 |
��3�����ӽ�PO�����P������Ϊ��t��-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
����P�ֱ��� x�ᣬy�������ߣ�����ֱ�ΪN��G��
�ɣ�1��֪����D������Ϊ��0��
| 3 |

��S�ı���PDBC=S��POC+S��POD+S��BOD
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
=-
| ||
| 2 |
| 3 |
| 2 |
25
| ||
| 8 |
�ʵ�t=
| 3 |
| 2 |
25
| ||
| 8 |
��ʱ��P������Ϊ��
| 3 |
| 2 |
5
| ||
| 4 |
���������⿼���˴���ϵ���������Ľ���ʽ���������ܳ���Сֵ�����Լ��ı��������Сֵ���⣮�����ۺ��Ժ�ǿ���ѶȺܴ���Ĺؼ���ע�����ν��˼���뷽��˼���Ӧ�ã�ע��ȷ���������ߣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
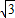 ������ABC=30°����������y=ax2+bx+cǡ�ù�A��B��C���㣬����y�ύ�ڵ�D��
������ABC=30°����������y=ax2+bx+cǡ�ù�A��B��C���㣬����y�ύ�ڵ�D��
 ������ABC=30°����������y=ax2+bx+cǡ�ù�A��B��C���㣬����y�ύ�ڵ�D��
������ABC=30°����������y=ax2+bx+cǡ�ù�A��B��C���㣬����y�ύ�ڵ�D��