题目内容
已知x、y、a都是实数,且|x|=1﹣a,y2=(1﹣a)(a﹣1﹣a2),则x+y+a3+1的值为 .
2
试题分析:根据绝对值非负数,平方数非负数的性质可得1﹣a=0,从而得到a的值,然后代入求出x、y的值,再把a、x、y的值代入代数式进行计算即可求解.
解:∵|x|=1﹣a≥0,
∴a﹣1≤0,﹣a2≤0,
∴a﹣1﹣a2≤0,
又y2=(1﹣a)(a﹣1﹣a2)≥0,
∴1﹣a=0,
解得a=1,
∴|x|=1﹣1=0,
x=0,
y2=(1﹣a)(﹣1﹣a2)=0,
∴x+y+a3+1=0+0+1+1=2.
故答案为:2.
点评:本题主要考查了代数式求值问题,把y2的多项式整理,然后根据非负数的性质求出a的值是解题的关键,也是解决本题的突破口,本题灵活性较强.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
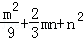
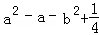 = .
= . abc2)2= _________ ;
abc2)2= _________ ; ,则
,则 ( )
( )

