题目内容
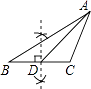
【题目】如图△ABC中,BE是∠ABC的外角平分线,BE交AC的延长线于E,∠A=∠E,求证:∠ACB=3∠A. 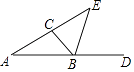
【答案】证明:∵BE是∠ABC的外角平分线, ∴∠EBD=∠EBC,
∵∠A=∠E,
∴∠EBD=∠EBC=∠A+∠E=2∠A,
∵∠ACB=∠E+∠EBC,
∴∠ACB=3∠A
【解析】根据角平分线定义求出∠EBD=∠EBC,根据角平分线性质得出∠EBD=∠EBC=∠A+∠E,∠ACB=∠E+∠EBC,即可求出答案.
【考点精析】根据题目的已知条件,利用三角形的外角的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目