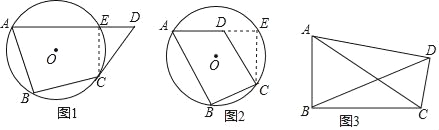
��Ŀ����
����Ŀ��ij��������˾������A,B�����ͺŵ�����Դ����10��.���������ṩ���������ֹ���:
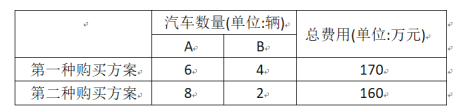
(1)A,B�����ͺŵ�����Դ����ÿ���ļ۸���Ƕ�����Ԫ?
(2)Ϊ��֧������Դ������ҵ�ķ�չ�����Ҷ�����Դ��������һ���IJ���.��֪���Ҷ�A, B�����ͺŵ�����Դ���������ʽ�ֱ�Ϊÿ��3��Ԫ��4��Ԫ.ͨ�����㣬����������˾�ڴ˴ι��������У����Ի�ù��Ҳ����ʽ�����34��Ԫ����˾��Ҫ֧���ʽ���145��Ԫ������ͨ����������м��ֹ���.
���𰸡���1����A�ͺŵ�����Դ����ÿ���۸�15��Ԫ��B�ͺŵ�����Դ����ÿ���۸�20��Ԫ����2�������ֹ���.
��������
��1���ֱ���A��B�ͺŵ�����Դ����ÿ���ļ۸�Ϊx��y��Ԫ�����ݱ�����г�һ����Ԫһ�η����飬��˷����鼴�ɵó��𰸣�
��2���蹺��A�ͳ�a��������B�ͳ�(10-a)��������������г�һ��һԪһ�β���ʽ�飬��˲���ʽ�飬ȡ�������⣬���ɵó���.
�⣺��1����A�ͺŵ�����Դ����ÿ���۸�x��Ԫ��B�ͺŵ�����Դ����ÿ���۸�y��Ԫ.
������ɵã�![]()
��ã�![]()
��A�ͺŵ�����Դ����ÿ���۸�15��Ԫ��B�ͺŵ�����Դ����ÿ���۸�20��Ԫ.
��2���蹺��A�ͳ�a��������B�ͳ�(10-a)��.
������ɵ�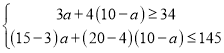
��ã�![]()
��a��ȡֵΪ4��5��6.
��������ֹ���.

����Ŀ��ѧУΪ����ͬѧ������ٳ��������μ����������������ˡ�ѧ�����������˶����������������������˶��б����μ��˰���ѵ��С�飮�ڽ����ΰ���ѵ���У��������������˵IJ��Գɼ�������ͳ�ƺͷ����������ͼ���е���Ϣ����������⣺
ƽ���� | ��λ�� | ���� | |
���� | 13.3 | 0.004 | |
���� | 13.3 | 0.02 |
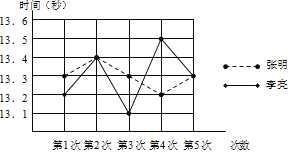
��1��������2�εijɼ�Ϊ�����������룻
��2�������ɼ���ƽ����Ϊ�����������������ɼ�����λ��Ϊ������������
��3�����ڴ�������������ѡ��һ���ɼ������ȥ�μӱ��������������ǵĽ�����Ӧ��ѡ��˭����˵�����ɣ�