题目内容
将正方形A的一个顶点与正方形B的对角线交叉重合,如图1位置,则阴影部分面积是正方形A面积的| 1 | 8 |
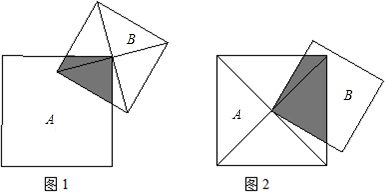
分析:本题考查了正方形的性质,全等三角形的判定,等腰直角三角形的性质.
解答:解:在图1中,∠GBF+∠DBF=∠CBD+∠DBF=90°,
∴∠GBF=∠CBD,∠BGF=∠CDB=45°,BD=BG,
∴△FBG≌△CBD,
∴阴影部分的面积等于△DGB的面积,且是小正方形的面积的
,是大正方形的面积的
;
设小正方形的边长为x,大正方形的边长为y,则有
x2=
y2,
∴y=
x,
同上,在图2中,阴影部分的面积是大正方形的面积的
,为
y2=
x2,
∴阴影部分面积是正方形B面积的
.
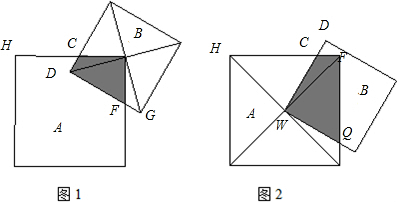
∴∠GBF=∠CBD,∠BGF=∠CDB=45°,BD=BG,
∴△FBG≌△CBD,
∴阴影部分的面积等于△DGB的面积,且是小正方形的面积的
| 1 |
| 4 |
| 1 |
| 8 |
设小正方形的边长为x,大正方形的边长为y,则有
| 1 |
| 4 |
| 1 |
| 8 |
∴y=
| 2 |
同上,在图2中,阴影部分的面积是大正方形的面积的
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴阴影部分面积是正方形B面积的
| 1 |
| 2 |

点评:本题是一道根据正方形的性质、全等三角形的判定和等腰直角三角形的性质结合求解的综合题.难度大,考查学生综合运用数学知识的能力.

练习册系列答案
相关题目

 ,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的_________
,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的_________ 
 ,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的_________
,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的_________ 
 ,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的 .
,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的 .