题目内容
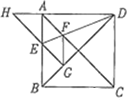
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:①DE平分∠ADB;②BE=2-![]() ;③四边形AEGF是菱形;④BC+FG=1.5.其中结论正确的序号是_______.
;③四边形AEGF是菱形;④BC+FG=1.5.其中结论正确的序号是_______.
【答案】①②③
【解析】
根据旋转的性质可知,△DGH≌△DCB,进而得知DH=DB,∠H=∠CBD=45°,∠DGH=∠DCB=90°,DG=DC=AD,之后可证△ADF≌△GDF,四边形AEGF是菱形,再根据勾股定理可知AE的长度,进而可以一一判断选出答案.
解:根据旋转的性质可知,△DGH≌△DCB,
∴DH=DB,∠H=∠CBD=45°,∠DGH=∠DCB=90°,DG=DC=AD,
在Rt△AED与Rt△GED中,AD=DG,ED=ED
∴Rt△AED≌Rt△GED(HL)
∴∠ADE=∠GDE,即DE平分∠ADB,故①正确;
在△ADF和△GDF中,AD=DG,∠ADF=∠GDF,DF=DF,
∴△ADF≌△GDF(SAS)
∴AF=GF,∠DAF=∠DGF=45°
又∵∠ABD=45°
∴FG∥AE
∵∠DAC=45°,
∴∠DAC=∠H,
∴AF∥EG
∴四边形AEGF是平行四边形,
又∵AF=GF
∴平行四边形AEGF是菱形,故③正确;
∵∠H=45°,∠HAE=90°
∴AE=AH
∵AE=AF=HD-AD=BD-AD
∵正方形ABCD的边长为1,根据勾股定理可知![]()
即HD=![]()
∴AE=![]()
∴BE=![]() ,故②正确;
,故②正确;
∵四边形AEGF是菱形
∴FG=AE=![]()
∴BC+FG=![]() ,故④错误;
,故④错误;
综上答案为①②③.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.