题目内容

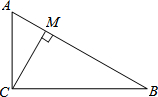
如图，在△ABC中，∠ACB=90°，CD⊥AB于D，∠A=30°，则AD等于（　　）
A．4BDB．3BDC．2BDD．BD

设BC=1，∠ACB=90°，∠A=30°，则AB=2BC=2，
根据勾股定理得：AC=
3
，
∵CD⊥AB，∴△ADC为直角三角形，
又∠A=30°，∴CD=
1
2
AC=
3
2
，
在直角△ADC中，根据勾股定理得：AD=
(
3
)2-(
3
2
)2
=
3
2
，
由∠ACB=90°，∠A=30°得到∠B=60°，∠CDB=90°，则∠BCD=30°，
∴BD=
1
2
BC=
1
2
，
则
AD
BD
=
3
2
1
2
=3，即AD=3BD．
故选B．
练习册系列答案
相关题目
△ABC中，AB=AC=30，∠BAC=150°，则△ABC的面积是______．
（1）如图1，△ABC中，∠BAC=90°，AB=AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD=DE+CE．
（2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．
如图1，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE．
（1）求证：S△ABD=S△ACE；
（2）如图2，AM是△ACE的中线，MA的延长线交BD于N，求证：MN⊥BD．
在Rt△ABC中，如果斜边上的中线CD=5cm，那么AB=______cm．
如图，将圆桶中的水倒入一个直径为40cm，高为55cm的圆口容器中，圆桶放置的角度与水平线的夹角为45度．若使容器中的水面与圆桶相接触，则容器中水的深度至少应为（　　）
A．10cmB．20cmC．30cmD．35cm
如图，△ABC中，∠ACB=90°，CM是高，∠B=30°．求证：AM=
1
4
AB．
一个等腰三角形，三个内角度数比为1：1：10，腰长为10cm，则这个三角形的面积是______．
小明、小敏两人一起做数学作业，小敏把题读到如图（1）所示，CD⊥AB，BE⊥AC时，还没把题读完，就说：“这题一定是求证∠B=∠C，也太容易了．”她的证法是：由CD⊥AB，BE⊥AC，得∠ADC=∠AEB=90°，公共角∠DAC=∠BAE，所以△DAC≌△EAB．由全等三角形的对应角相等得∠B=∠C．
小明说：“小敏你错了，你未弄清本题的条件和结论，即使有CD⊥AB，BE⊥AC，公共角∠DAC=∠BAE，你的推理也是错误的．看我画的图（2），显然△DAC与△EAB是不全等的．再说本题不是要证明∠B=∠C，而是要证明BE=CD．”
（1）根据小敏所读的题，判断“∠B=∠C”对吗？她的推理对吗？若不对，请做出正确的推理．
（2）根据小明说的，要证明BE=CD，必然是小敏丢了题中条件，请你把小敏丢的条件找回来，并根据找出的条件，你做出判断BE=CD的正确推理．
（3）要判断三角形全等，从这个问题中你得到了什么启发？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网