题目内容
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
①△ABD是正三角形;②若AF=2DF,则EG=2DG;③△AED≌△DFB;④S四边形BCDG=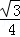 CG2;
CG2;
其中正确的结论是 .
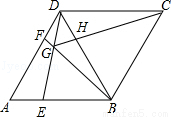
①③④.
【解析】
试题分析:
①∵ABCD为菱形,∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
故本小题正确;
②过点F作FP∥AE于P点,
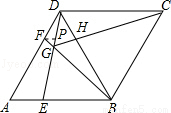
DP:PE=DF:DA=1:2,
而点G与点P不重合,否则与与原题矛盾,
所以EG=2DG错误;
③∵△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故本小题正确;
④∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
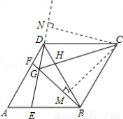
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM= CG,CM=
CG,CM=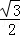 CG,
CG,
∴S四边形CMGN=2S△CMG=2× ×
×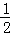 CG×
CG× CG=
CG=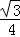 CG2,故本小题正确;
CG2,故本小题正确;
综上所述,正确的结论有①③④.
故答案为:①③④.
考点:菱形的性质;全等三角形的判定与性质.

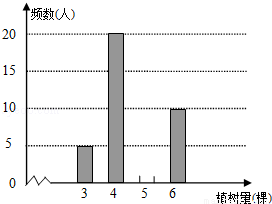
今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
植树数量(棵) | 频数(人) | 频率
|
3 | 5 | 0.1 |
4 | 20 | 0.4 |
5 |
|
|
6 | 10 | 0.2 |
合计 | 50 | 1 |
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的众数和中位数,并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量.