题目内容
 如图,填空:
如图,填空:(1)如果∠1=∠2,那么根据
内错角相等两直线平行
内错角相等两直线平行
,可得AB
AB
∥CD
CD
;(2)如果∠DAB+∠ABC=180°,那么根据
同旁内角互补两直线平行
同旁内角互补两直线平行
,可得AD
AD
∥BC
BC
;(3)当
AB
AB
∥CD
CD
时,根据两直线平行同旁内角互补
两直线平行同旁内角互补
,可得∠C+∠ABC=180°;(4)当
AD
AD
∥BC
BC
时,根据两直线平行内错角相等
两直线平行内错角相等
,可得∠C=∠3.分析:(1)利用内错角相等两直线平行得到AB与CD平行;
(2)利用同旁内角互补两直线平行得到AD与BC平行;
(3)根据AB与CD平行,利用两直线平行同旁内角互补即可得到;
(4)由AD与BC平行,利用两直线平行内错角相等即可得到.
(2)利用同旁内角互补两直线平行得到AD与BC平行;
(3)根据AB与CD平行,利用两直线平行同旁内角互补即可得到;
(4)由AD与BC平行,利用两直线平行内错角相等即可得到.
解答:解:(1)如果∠1=∠2,那么根据内错角相等两直线平行,可得AB∥CD;
(2)如果∠DAB+∠ABC=180°,那么根据同旁内角互补两直线平行,可得AD∥BC;
(3)当AB∥CD时,根据两直线平行同旁内角互补,可得∠C+∠ABC=180°;
(4)当AD∥BC时,根据两直线平行内错角相等,可得∠C=∠3.
故答案为:(1)内错角相等两直线平行,AB,CD;(2)同旁内角互补两直线平行,AD,BC;(3)AB,CD,两直线平行同旁内角互补;(4)AD,BC,两直线平行内错角相等
(2)如果∠DAB+∠ABC=180°,那么根据同旁内角互补两直线平行,可得AD∥BC;
(3)当AB∥CD时,根据两直线平行同旁内角互补,可得∠C+∠ABC=180°;
(4)当AD∥BC时,根据两直线平行内错角相等,可得∠C=∠3.
故答案为:(1)内错角相等两直线平行,AB,CD;(2)同旁内角互补两直线平行,AD,BC;(3)AB,CD,两直线平行同旁内角互补;(4)AD,BC,两直线平行内错角相等
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目

 6、如图,填空:(填SSS、SAS、ASA或AAS)
6、如图,填空:(填SSS、SAS、ASA或AAS)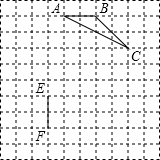 (2012•河池)如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上.
(2012•河池)如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上.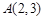 ,
,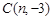 (其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.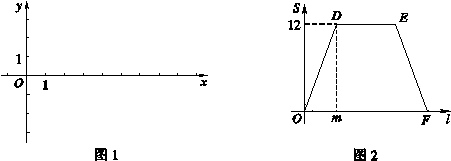
 图2中OF的长;
图2中OF的长; 上方的抛物线W上,坐标平面内另有一点R,满足以B,
上方的抛物线W上,坐标平面内另有一点R,满足以B,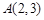 ,
,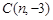 (其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.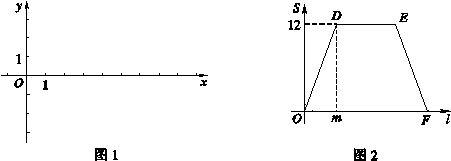
 图2中OF的长;
图2中OF的长;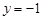 上方的抛物线W上,坐标平面内另有一点R,满足以B,
上方的抛物线W上,坐标平面内另有一点R,满足以B,