Question

已知：如图，AB是⊙O的直径，AC是⊙O的弦，过点C作⊙O的切线与AB的延长线交于点D。若∠CAB＝30°，AB＝30，求BD的长。

Answer 1

BD=15

试题分析：作辅助线，连接OC，根据已知条件，可知∠COD的度数和OC的长；在Rt△OCD中，根据三角函数，可将OD的长求出，进而可将BD的长求出
解：连接OC，

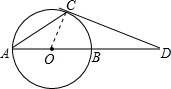
∵CD是⊙O的切线，
∴OC⊥CD，且OC=OA=OB=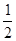AB=15，
∵∠CAB=30°，
∴∠COD=2∠CAB=60°，即∠D=30°，
∴在Rt△OCD中，OD=2OC=30，
∴BD=OD-OB=15．．
点评：解答本题的关键是知道运用切线的性质来进行计算或论证，常通作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．