题目内容
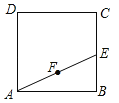
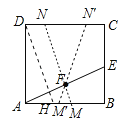
【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
【答案】![]() 或
或![]() .
.
【解析】
试题分析:如图,作DH∥MN,∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠B=90°,AB∥CD,∴四边形DHMN是平行四边形,∴DH=MN=AE,在RT△ADH和RT△BAE中,∵AD=AB,DH=AE,∴△ADH≌△BAE,∴∠ADH=∠BAE,∴∠ADH+∠AHD=∠ADH+∠AMN=90°,∴∠BAE+∠AMN=90°,∴∠AFM=90°,在RT△ABE中,∵∠B=90°,AB=![]() ,∠BAE=30°,∴AEcos30°=AB,∴AE=2,在RT△AFM中,∵∠AFM=90°,AF=1,∠FAM=30°,∴AMcos30°=AF,∴AM=
,∠BAE=30°,∴AEcos30°=AB,∴AE=2,在RT△AFM中,∵∠AFM=90°,AF=1,∠FAM=30°,∴AMcos30°=AF,∴AM=![]() ,根据对称性当M′N′=AE时,BM′=
,根据对称性当M′N′=AE时,BM′=![]() ,AM′=
,AM′=![]() .故答案为:
.故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目