题目内容
(2013•集美区一模)已知抛物线y1=-x2+bx+c(b≠0)与x轴正半轴交于A(c,0),与y轴交于B点,直线AB的解析式为y2=mx+n.
(1)求m-n+b的值;
(2)若抛物线顶点P关于y轴的对称点恰好在直线AB上,M是线段BA上的点,过点M作MN∥y轴交抛物线于点N.试问:当点M从点B运动到点A时,线段MN的长度如何变化?
(1)求m-n+b的值;
(2)若抛物线顶点P关于y轴的对称点恰好在直线AB上,M是线段BA上的点,过点M作MN∥y轴交抛物线于点N.试问:当点M从点B运动到点A时,线段MN的长度如何变化?
分析:(1)把点A的坐标代入抛物线解析式得到b=c-1;把点A、B的坐标分别代入直线AB的解析式求得m=-1,n=c,将其代入所求的代数式并求值即可;
(2)由(1)中的抛物线解析式可以求得顶点P(
,
),则易求顶点P关于y轴对称的点P′(
,
).由一次函数y2=-x+c图象上点的坐标特征可以
求得c=3.易求得y1=-x2+2x+3,y2=-x+3.则MN=-(x,所以由二次函数图象的性质进行解答即可.
(2)由(1)中的抛物线解析式可以求得顶点P(
| c-1 |
| 2 |
| c2+2c+1 |
| 4 |
| 1-c |
| 2 |
| c2+2c+1 |
| 4 |
求得c=3.易求得y1=-x2+2x+3,y2=-x+3.则MN=-(x,所以由二次函数图象的性质进行解答即可.
解答: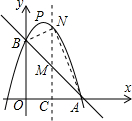 解:(1)把A(c,0)代入抛物线得:-c2+bc+c=0,
解:(1)把A(c,0)代入抛物线得:-c2+bc+c=0,
如图,∵A(c,0)在x轴正半轴,
∴c>0,
∴b=c-1,
∵抛物线与y轴交于B点.
∴B(0,c)
把A(c,0)、B(0,c)分别代入y2=mx+n得:
,
解得:
∴m-n+b=-1-c+c-1=-2;
(2)∴y1=-x2+(c-1)x+c,y2=-x+c
∴顶点P(
,
)
∴顶点P关于y轴对称的点P′(
,
)
把P′代入y2=-x+c得:
+c=
解得:c1=3,c2=1(舍去)
∴当c=3时,b=c-1=2;
当c=1时,b=0;
∵b≠0
∴c=3,b=2,
∴y1=-x2+2x+3,y2=-x+3
∵M是线段AB上的点,
∴y2≤y1,0≤x≤3.
∵MN∥y轴
∴MN=y1-y2=-x2+3x
∴MN=-(x
∵a=-1<0,开口向下,对称轴为x=
∴当0≤x≤
时,MN长度随着x增大而增大;
当
≤x≤3时,MN长度随着x增大而减小.
 解:(1)把A(c,0)代入抛物线得:-c2+bc+c=0,
解:(1)把A(c,0)代入抛物线得:-c2+bc+c=0,如图,∵A(c,0)在x轴正半轴,
∴c>0,
∴b=c-1,
∵抛物线与y轴交于B点.
∴B(0,c)
把A(c,0)、B(0,c)分别代入y2=mx+n得:
|
解得:
|
∴m-n+b=-1-c+c-1=-2;
(2)∴y1=-x2+(c-1)x+c,y2=-x+c
∴顶点P(
| c-1 |
| 2 |
| c2+2c+1 |
| 4 |
∴顶点P关于y轴对称的点P′(
| 1-c |
| 2 |
| c2+2c+1 |
| 4 |
把P′代入y2=-x+c得:
| c-1 |
| 2 |
| c2+2c+1 |
| 4 |
解得:c1=3,c2=1(舍去)
∴当c=3时,b=c-1=2;
当c=1时,b=0;
∵b≠0
∴c=3,b=2,
∴y1=-x2+2x+3,y2=-x+3
∵M是线段AB上的点,
∴y2≤y1,0≤x≤3.
∵MN∥y轴
∴MN=y1-y2=-x2+3x
∴MN=-(x
∵a=-1<0,开口向下,对称轴为x=
| 3 |
| 2 |
∴当0≤x≤
| 3 |
| 2 |
当
| 3 |
| 2 |
点评:本题综合考查了一次函数、二次函数图象上点的坐标特征,待定系数法求一次函数、二次函数的解析式以及二次函数图象的性质.综合性强,要求学生掌握数形结合的数学思想方法.(2)中弄清线段MN长度的函数意义是解题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目