题目内容
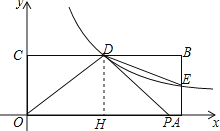
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=![]() .
.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.

【答案】(1)![]() (2)3(3)P点的坐标是(4,0)或(
(2)3(3)P点的坐标是(4,0)或(![]() ,0).
,0).
【解析】
(1)由四边形OABC是矩形,得到BC=OA,AB=OC,根据tan∠COD=![]() ,设OC=3x,CD=4x,求出OD=5x=5,OC=3,CD=4,得到D(4,3),代入反比例函数的解析式即可.
,设OC=3x,CD=4x,求出OD=5x=5,OC=3,CD=4,得到D(4,3),代入反比例函数的解析式即可.
(2)根据D点的坐标求出点B,E的坐标即可求出结论;
(3)分类讨论:当∠OPD=90°时,过D作PD⊥x轴于P,点P即为所求,当∠ODP=90°时,根据射影定理即可求得结果.
(1)∵四边形OABC是矩形,
∴BC=OA,AB=OC,
∵tan∠COD=![]() ,
,
∴设OC=3x,CD=4x,
∴OD=5x=5,
∴x=1,
∴OC=3,CD=4,
∴D(4,3),
设过点D的反比例函数的解析式为:y=![]() ,
,
∴k=12,
∴反比例函数的解析式为:y=![]() ;
;
(2)∵点D是BC的中点,
∴B(8,3),
∴BC=8,AB=3,
∵E点在过点D的反比例函数图象上,
∴E(8,![]() ),
),
∴S△DBE=![]() BDBE=
BDBE=![]() =3;
=3;
(3)存在,
∵△OPD为直角三角形,
∴当∠OPD=90°时,PD⊥x轴于P,
∴OP=4,
∴P(4,0),
当∠ODP=90°时,
如图,过D作DH⊥x轴于H,
∴OD2=OHOP,
∴OP=![]() .
.
∴P(![]() ,O),
,O),
∴存在点P使△OPD为直角三角形,
∴P(4,O),(![]() ,O).
,O).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目