题目内容
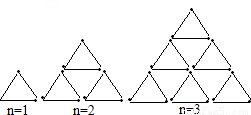
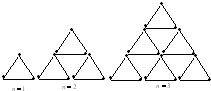18、如图：是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，当每边上摆20（即n=20）根时，需要的火柴棍总数为630
根．分析：关键是通过归纳与总结，得到其中的规律，按规律求解．
解答：解：n=1时，有1个三角形，需要火柴的根数为：3×1；
n=2时，有3个三角形，需要火柴的根数为：3×（1+2）；
n=3时，有6个三角形，需要火柴的根数为：3×（1+2+3）；
…；
n=20时，需要火柴的根数为：3×（1+2+3+4+…+20）=630．
故答案为：630．
n=2时，有3个三角形，需要火柴的根数为：3×（1+2）；
n=3时，有6个三角形，需要火柴的根数为：3×（1+2+3）；
…；
n=20时，需要火柴的根数为：3×（1+2+3+4+…+20）=630．
故答案为：630．
点评：此题考查的知识点是图形数字的变化类问题，本题的关键是弄清到底有几个小三角形．
练习册系列答案
相关题目
16、如图，是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，当边上摆8（即n=8）根时，需要的火柴总数为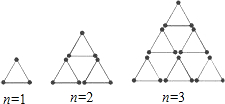
如图，是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，摆第5个图形时，需要的火柴棍为
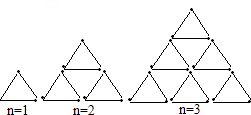如图：是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，当每边上摆6（即n=6）根时，需要的火柴棍总数为