题目内容
(2000•宁波)已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC.求证:AC=DB.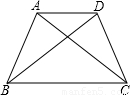
【答案】分析:因为ABCD是等腰梯形,则∠ABC=∠DCB,再根据SAS判定△ABC≌△DCB即可得出AC=BD.
解答:证明:∵四边形ABCD是等腰梯形,
∴∠ABC=∠DCB.(2分)
在△ABC和△DCB中,
AB=DC,∠ABC=∠DCB,BC=CB,(3分)
∴△ABC≌△DCB.(1分)
∴AC=BD.(2分)
点评:此题主要考查了等腰梯形的性质及全等三角形的判定方法的运用.
解答:证明:∵四边形ABCD是等腰梯形,
∴∠ABC=∠DCB.(2分)
在△ABC和△DCB中,
AB=DC,∠ABC=∠DCB,BC=CB,(3分)
∴△ABC≌△DCB.(1分)
∴AC=BD.(2分)
点评:此题主要考查了等腰梯形的性质及全等三角形的判定方法的运用.

练习册系列答案
相关题目
