题目内容
【题目】如图，在菱形ABCD中，AB=6，∠B=60°，点G是边CD边的中点，点E、F分别是AG、AD上的两个动点，则EF+ED的最小值是 ．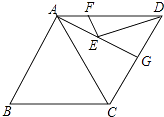 
【答案】3 
【解析】解：如图作DH⊥AC垂足为H与AG交于点E，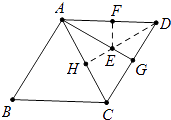
∵四边形ABCD是菱形，
∵AB=AD=CD=BC=6，
∵∠B=60°，
∴∠ADC=∠B=60°，
∴△ADC是等边三角形，
∵AG是中线，
∴∠GAD=∠GAC
∴点H关于AG的对称点F在AD上，此时EF+ED最小=DH．
在RT△DHC中，∵∠DHC=90°，DC=6，∠CDH= 
∠ADC=30°，
∴CH= DC=3，DH= 
= 
=3 ，
∴EF+DE的最小值=DH=3
故答案为3 ．
作DH⊥AC垂足为H与AG交于点E，点H关于AG的对称点为F，此时EF+ED最小=DH，先证明△ADC是等边三角形，在RT△DCH中利用勾股定理即可解决问题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】在平面内,分别用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下.
火柴棒数 | 3 | 5 | 6 | … |
示意图 |
|
|
| … |
形状 | 等边三角形 | 等腰三角形 | 等边三角形 | … |
问:(1)4根火柴棒能搭成三角形吗?
(2)8根、12根火柴棒分别能搭成几种不同形状的三角形?并画出它们的示意图.
