��Ŀ����
����Ŀ����ͼ��AB��CD������E��F�ֱ���ֱ��AB��CD�ϣ�ƽ����AB��CD֮����һ����P��
��1����ͼ1����P����EF�����ʱ����AEP����EPF����PFC����������ϵΪ�� ������ͼ2����P����EF���Ҳ�ʱ����AEP����EPF����PFC����������ϵΪ�� ����
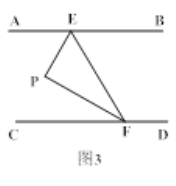
��2����ͼ3������EPF��90�㣬FPƽ�֡�EFCʱ����֤��EPƽ�֡�AEF��
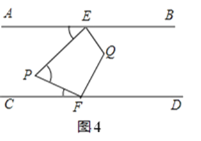
��3����ͼ4��QE��QF�ֱ�ƽ�֡�PEB�͡�PFD���ҵ�P��EF��࣮
������EPF��60�㣬���EQF���� ����
�������EPF���EQF��������ϵ����˵�����ɣ�
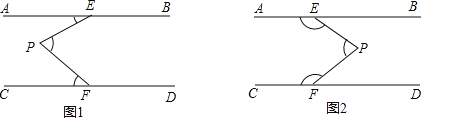
���𰸡���1����EPF=��AEP+��PFC����AEP+��EPF+��PFC=360�㣻��2������������3����150�㣬��EQF=180�㣭![]() ��EPF
��EPF
��������
��1������ͼ������P��AB��ƽ���ߣ�����ƽ���ߵ����ʿ��Ƶ����Ƕȹ�ϵ��
��2������ͼ�����ݣ�1���Ľ��ۣ��ɵá�AEP+��PFC=��EPF=90�������á�EPF�ڽǺ�Ϊ180�����Ƶ��ó���PEF+��PFE=90�����Ӷ��ó���PEF=��AEP��
��3�������ݣ�1���Ľ���֪����AEP+��PFC=��EPF=60���������ý�ƽ���ߵ����ʵó���PEQ+��PFQ=150����������ı���EPFQ�еó����ۣ�
�ڸ��ݣ�1���Ľ���֪����AEP+��PFC=��EPF���������ý�ƽ���ߵ����ʵó���PEQ+��PFQ=180����![]() ��������ı���EPFQ�еó����ۣ�
��������ı���EPFQ�еó����ۣ�
��1������ͼ������P��PQ��AB

��PQ��AB��AB��CD����PQ��CD
���AEP=��EPQ����QPF=��PFC
�֡ߡ�EPF=��EPQ+��QPF
���EPF=��AEP+��PFC
����ͼ������P��PQ��AB
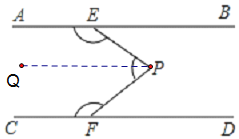
ͬ����AB��QP��CD
���AEP+��QPE=180������QPF+��PFC=180��
���AEP+��EPF+��PFC=��AEP+��EPQ+��QPF+��PFC=360��
��2�����ݣ�1���Ľ���֪����AEP+��PFC=��EPF=90��
��PF�ǡ�CFE�Ľ�ƽ���ߣ����PFC=��PFE
�ڡ�PEF�У��ߡ�EPF=90�������PEF+��PFE=90��
���PEF+��PFE=��AEP+��PFC
���PEF=��AEP����PE�ǡ�AEF�Ľ�ƽ����
��3�������ݣ�1���Ľ���֪����AEP+��PFC=��EPF=60��
���BEP+��PFD=180������AEP+180������PFC=300��
��EQ��QF�ֱ��ǡ�PEB�͡�PFD�Ľ�ƽ����
���PEQ=QEB����PFQ=��QFD
���PEQ+��PFQ=150��
���ı���PEQF�У���EQF=360������EPF��(��PEQ+��PFQ)=360����60����150��=150��
�ڸ��ݣ�1���Ľ���֪����AEP+��PFC=��EPF
���BEP+��PFD=180������AEP+180������PFC=360������EPF
��EQ��QF�ֱ��ǡ�PEB�͡�PFD�Ľ�ƽ����
���PEQ=��QEB����PFQ=��QFD
���PEQ+��PFQ=![]() =180����
=180����![]()
�����ı���PEQF�У�
��EQF=360������EPF��(��PEQ+��PFQ)=360����![]() ��(180����
��(180����![]() )=180����
)=180����![]()

����Ŀ��ijУ���꼶ѧ����չ�����������ÿ����5��ѧ���μӣ��������ֶܷ����������Σ�ͳ�Ʒ��ֳɼ���õļװ���Ұ��ܷ���ȣ��±��Ǽװ���Ұ�ѧ���ı�������![]() ��λ����
�����![]()
ѡ�� | 1�� | 2�� | 3�� | 4�� | 5�� | �ܼ� |
�װ� | 100 | 98 | 105 | 94 | 103 | 500 |
�Ұ� | 99 | 100 | 95 | 109 | 97 | 500 |
��ʱ��ѧ�����飬����ͨ�����������е�������Ϣ��Ϊ�ο��������������⣺
![]() ��������������е���λ�����Լ����
��������������е���λ�����Լ����
![]() ������������ݣ�˵��Ӧ�ö���һ����Ϊ�ھ���Ϊʲô��
������������ݣ�˵��Ӧ�ö���һ����Ϊ�ھ���Ϊʲô��