题目内容
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,点
上一点,点![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,在射线
两点,在射线![]() 上取点
上取点![]() ,使
,使![]() .
.

(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)当![]() 是
是![]() 的中点时;
的中点时;
①若![]() ,求证:以
,求证:以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形;
为顶点的四边形是菱形;
②若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①见解析,②5
【解析】
(1)如图1,连接OC.则OC=OB,根据等腰三角形的性质等边对等角可得:∠OBC=∠OCB.再由垂直的定义可得∠BPD=90°.又根据三角形的内角和定理可得∠OBC+∠BDP=90°.由FC=FD可得∠FCD=∠FDC.又因为∠FDC=∠BDP,所以
∠OCB+∠FCD=90°,从而可证明.
(2)①如图2,连接OE,BE,CE.先由已知条件证出△BOE,△OCE均为等边三角形,再根据等边三角形的三条边相等可证得:OB=BE=CE=OC,从而根据四条边相等的四边形是菱形可证得结果.
②构造直角三角形,利用三角函数和勾股定理求即可.
(1)证明:如图1,连接OC.
∵OB=OC,∴∠OBC=∠OCB.
∵PF⊥AB,∴∠BPD=90°.∴∠OBC+∠BDP=90°.
∵FC=FD,∴∠FCD=∠FDC.
又∵∠FDC=∠BDP,
∴∠OCB+∠FCD=90°,即∠OCF=90°.
∴FC是⊙O的切线.
图1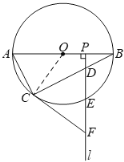
(2)①证明:如图2,连接OE,BE,CE.
∵AB是⊙O的直径,∴∠ACB=90°.
∵∠BAC=60°,∴∠BOC=2∠BAC=120°.
∵E是![]() 的中点,即
的中点,即![]() ,
,
∴∠BOE=∠COE=60°.
又∵OB=OE=OC,∴△BOE,△OCE均为等边三角形.
∴OB=BE=CE=OC.∴四边形BOCE是菱形.
②解:如图2,记OE与BC的交点为H.
∵AB是⊙O的直径,∴∠ACB=90°.
∴在Rt△ABC中,tan∠ABC=![]() =
=![]() .
.
设AC=3k,BC=4k(k>0).
∵AC2+BC2=AB2,
∴(3k)2+(4k)2=202,解得k=4.
∴AC=12,BC=16.
∵E是![]() 的中点,OE是⊙O的半径,
的中点,OE是⊙O的半径,
∴OE⊥BC,BH=CH=![]() BC=8.
BC=8.
∵S△BOE=![]() OE·BH=
OE·BH=![]() OB·PE,OE=OB=
OB·PE,OE=OB=![]() AB=10,
AB=10,
∴PE=![]() =
=![]() =8.
=8.
在Rt△OPE中,OP=![]() =
=![]() =6.
=6.
∴BP=OB-OP=10-6=4.
在Rt△BPD中,![]() =tan∠ABC=
=tan∠ABC=![]() ,∴DP=
,∴DP=![]() BP=
BP=![]() ×4=3.
×4=3.
∴DE=PE-DP=8-3=5.
图2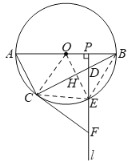
【点晴】
本题是圆的综合题,难度较大,灵活运用知识作出合理的辅助线构造直角三角形是解题的关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案【题目】为了了解某区九年级数学教学质量检测情况,进行了抽样调查,其过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:随机抽取甲、乙两所学校中各自取20名学生的数学成绩进行分析
甲:91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙:84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理数据:表一
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 2 | 8 | 5 |
分析数据:表二
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 115.25 |
得出结论:
(1)若甲学校有400名九年级学生,估计这次考试成绩80分(包含80分)以上人数为 .
(2)可以推断出 (填:甲或乙)学校学生的数学水平较高,理由是 (至少从两个不同角度说明推断的合理性).