题目内容
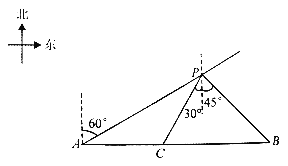
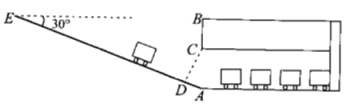
【题目】如下图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米.地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米,![]() ).
).
【答案】6.8(米);![]() (米)
(米)
【解析】
根据直角三角形中边角关系和特殊角的锐角函数值,过C点作AE边的垂线,构建出AC所在的直角三角形,然后通过设出AC的长度,表示出AB的长度,利用直角三角形中边角关系即可求出AC的长度,同样在直角三角形ACD中,利用边角关系即可求出CD的长度.
解:过C点向AE作垂线,垂足为D,
设AC=x,则AB的长为(x+1.2)米,
在Rt△ABE中,∠E=30°,AE=12
根据直角三角形边角关系可得:![]() ,
,
∴x=6.8
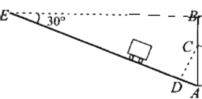
∵∠E=30°,
∴∠A=60°,
在Rt△ACD中,
![]() (米)
(米)

练习册系列答案
相关题目