题目内容
如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D地边AC上,点E、F在边AB上,点G在边BC上。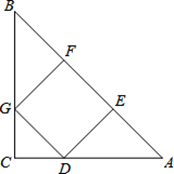
(1)求证:△ADE≌△BGF;
(2)若正方形DEFG的面积为16cm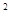 ,求AC的长。
,求AC的长。
解:(1)证明:∵△ABC是等腰直角三角形,∠C=90°,
∴∠B=∠A=45°。
∵四边形DEFG是正方形,∴∠BFG=∠AED=90°。
∴∠BGF=∠ADE=45°,GF=ED。
∵在△ADE与△BGF中, ,
,
∴△ADE≌△BGF(ASA)。
(2)如图,过点C作CG⊥AB于点G,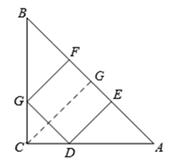
∵正方形DEFG的面积为16cm2,∴DE=AE=4cm。
∴AB=3DE=12cm。
∵△ABC是等腰直角三角形,CG⊥AB,
∴AG= AB=
AB= ×12=6cm。
×12=6cm。
在Rt△ADE中,∵DE=AE=4cm,
∴ (cm)。
(cm)。
∵CG⊥AB,DE⊥AB,∴CG∥DE。∴△ADE∽△ACG。
∴ ,即
,即 ,解得
,解得 cm。
cm。
解析

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
如图,该几何体的左视图是( )
A. | B. | C. | D. |
如图,桌面上有一个一次性纸杯,它的正视图应是( )
A. | B. | C. | D. |


 时,求
时,求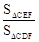 的值;
的值;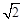 OA;
OA; BG.
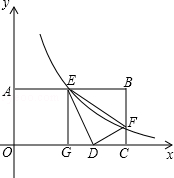
BG. (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.