题目内容
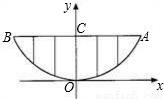
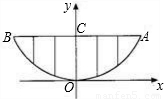 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,抛物线y=ax2中a=______;
(2)计算一段栅栏所需立柱的总长度为______米.(精确到0.1米)
【答案】分析:(1)这是抛物线解析式的最简形式,只需要已知抛物线上一个点的坐标,就可以求a,从而确定解析式;
(2)根据抛物线的对称性,求出每根栅栏下端的纵坐标,利用上端纵坐标-下端纵坐标=每根长度,然后求总长.
解答: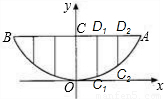 解:(1)由已知:OC=0.6,AC=0.6,
解:(1)由已知:OC=0.6,AC=0.6,
得点A的坐标为(0.6,0.6),
代入y=ax2,
得a= ,
,
∴抛物线的解析式为y= x2;
x2;
(2)点D1,D2的横坐标分别为0.2,0.4,
代入y= x2,
x2,
得点D1,D2的纵坐标分别为:
y1= ×0.22≈0.07,y2=
×0.22≈0.07,y2= ×0.42≈0.27,
×0.42≈0.27,
∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为:2(C1D1+C2D2)+OC=2(0.53+0.33)+0.6≈2.3米.
点评:会用抛物线解析式,求每根栅栏上下两端的纵坐标,用纵坐标的差,表示长度,用对称性求总长.
(2)根据抛物线的对称性,求出每根栅栏下端的纵坐标,利用上端纵坐标-下端纵坐标=每根长度,然后求总长.
解答:
 解:(1)由已知:OC=0.6,AC=0.6,
解:(1)由已知:OC=0.6,AC=0.6,得点A的坐标为(0.6,0.6),
代入y=ax2,
得a=
 ,
,∴抛物线的解析式为y=
 x2;
x2;(2)点D1,D2的横坐标分别为0.2,0.4,
代入y=
 x2,
x2,得点D1,D2的纵坐标分别为:
y1=
 ×0.22≈0.07,y2=
×0.22≈0.07,y2= ×0.42≈0.27,
×0.42≈0.27,∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为:2(C1D1+C2D2)+OC=2(0.53+0.33)+0.6≈2.3米.
点评:会用抛物线解析式,求每根栅栏上下两端的纵坐标,用纵坐标的差,表示长度,用对称性求总长.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
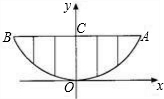 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )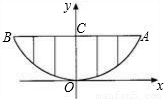 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米. 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.