题目内容
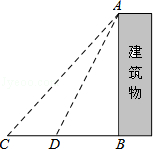
【题目】如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( ) 
A.50°
B.60°
C.70°
D.80°
【答案】B
【解析】解:四边形纸片ABCD中,∠A=70°,∠B=80°, ∴∠D+∠C=360°﹣∠A﹣∠B=210°,
∵将纸片折叠,使C,D落在AB边上的C,D′处,
∴∠MD′B=∠D,∠NC′A=∠C,
∴∠MD′B+∠NC′A=210,
∴∠AD′M+∠BC′N=150°,
∴∠AMD′+∠BNC′=360°﹣∠A﹣∠B﹣∠AD′M﹣∠BC′N=60°,
故选B.
根据四边形的内角和得到∠D+∠C=360°﹣∠A﹣∠B=210°,由折叠的性质得到∠MD′B=∠D,∠NC′A=∠C,得到∠MD′B+∠NC′A=210,根据平角的定义得到∠AD′M+∠BN′N=150°,根据三角形的内角和即可得到结论.

练习册系列答案
相关题目
【题目】学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖 | 二等奖 | 三等奖 |
1盒福娃和1枚徽章 | 1盒福娃 | 1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:
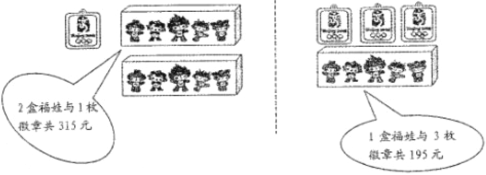
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?