题目内容
如图所示，点C是线段AB上的点，点D是线段BC的中点，若AB=12，AC=8，求CD的值．
解：∵AB=12，AC=8，
∴BC=AB-AC=4．
∵点D是线段BC的中点，
∴CD=
BC=4，即线段CD的值是4．
分析：由图示知BC=AB-AC=4．然后由线段中点的定义易求CD=BC=4，即线段CD的值是4．
点评：本题考查了两点间的距离．此题是根据图形求得相关线段间的和差倍分的数量关系．
∴BC=AB-AC=4．
∵点D是线段BC的中点，
∴CD=
BC=4，即线段CD的值是4．分析：由图示知BC=AB-AC=4．然后由线段中点的定义易求CD=
BC=4，即线段CD的值是4．点评：本题考查了两点间的距离．此题是根据图形求得相关线段间的和差倍分的数量关系．
练习册系列答案
相关题目
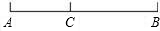如图所示，点C是线段AB的黄金分割点，且AC＜BC，AC=mBC，则m的值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示，点C是线段AB上的点，点D是线段BC的中点，若AB=12，AC=8，求CD的值．
如图所示，点C是线段AB的中点，BD=
