题目内容
【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧![]() 围成的弓形面积.
围成的弓形面积.
【答案】(1)证明见解析;(2)![]()
【解析】本题主要考查了二次函数与一元二次方程的联系、根的判别式、函数图象与坐标轴交点坐标的求法、函数解析式的确定、扇形面积的计算方法等
(1)若抛物线于x轴有交点,那么当y=0时,所得方程的根的判别式恒大于等于0,可据此进行证明;将抛物线解析式的右边,用十字相乘法进行因式分解,可得:y=(mx-5)(x-1),由此可看出抛物线一定经过点(1,0).
(2)由于抛物线交x轴于A、B两点,且A在B左侧,且A、B都在原点的右侧,因此A(1,0),B(5,0),根据A点坐标,可确定直线的解析式,根据A、B的坐标,可确定抛物线的解析式;
若⊙M同时经过A、B两点,根据抛物线和圆的对称性知:点M必为抛物线对称轴与直线的交点,由此可求得点M的坐标为(3,2),而AB=4,因此△ABM是个等腰直角三角形,即可得到![]() 的圆心角,那么扇形MAB的面积减去等腰直角三角形MAB的面积即为所求弓形的面积.
的圆心角,那么扇形MAB的面积减去等腰直角三角形MAB的面积即为所求弓形的面积.
(1)证明:∵y=mx2-(m+5)x+5,∴△=[-(m+5)]2-4m×5=m2+10m+25-20m="(m-" 5)2.
不论m取任何实数,(m-5)2≥0,即△≥0,故抛物线与x轴必有交点.
又∵x轴上点的纵坐标均为零,∴令y=0,代入y=mx2-(m+5)x+5,得
mx2-(m+5)x+ 5=0,(mx-5)(x-1)=0,
∴x=![]() 或x=1.故抛物线必过x轴上定点(1,0).
或x=1.故抛物线必过x轴上定点(1,0).
(2)解:如答图所示,
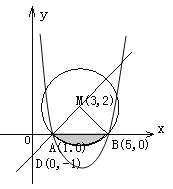
∵L:y=x+k,把(1,0)代入上式,
得0=1+k,∴k=-1,∴y="x-1."
又∵抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,AB=4,
∵x1x2>0,∴x1="1," x2=5,∴A(1,0),B(5,0),
把B(5,0)代入y=mx2-(m+5)x+5,得0=25m-(m+5)×5+5.
∴m=1,∴y=x2-6x+5.
∵M点既在直线L:y=x-1上,又在线段AB的垂直平分线上,
∴M点的横坐标x1+![]() =1+
=1+![]() .
.
把x=3代入y=x-1,得y=2.
∴圆心M(3,2),∴半径r=MA=MB=![]() ,
,
∴MA2=MB2=8.
又AB2=42= 16,∴MA2+MB2=AB2,
∴△ABM为直角三角形,且∠AMB=90°,
∴S弓形ACB=S扇形AMB- S△ABM=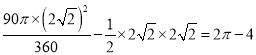 .
.

 高中必刷题系列答案
高中必刷题系列答案