题目内容
(2012•历下区二模)(1)已知:如图1,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE=DF.
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是
的中点,过点D作直线BC的垂线,分别交CB,CA的延长线于E,F,求证:EF是⊙O的切线.
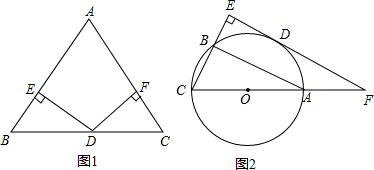
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是
 | AB |

分析:(1)连接AD,根据等腰三角形的三线合一定理得出AD平分∠BAC,根据角平分线性质得出DE=DF即可;
(2)连接OD,根据圆周角定理得出BA⊥BC,推出EF∥AB,根据垂径定理得出OD⊥AB,即可得出OD⊥EF,根据切线的判定推出即可.
(2)连接OD,根据圆周角定理得出BA⊥BC,推出EF∥AB,根据垂径定理得出OD⊥AB,即可得出OD⊥EF,根据切线的判定推出即可.
解答:
(1)证明:连接AD,
∵AB=AC,D为BC中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)证明:连接OD交AB于M,
∵D为弧AB中点,OD为半径,
∴OD⊥AB,
∵AC为直径,
∴∠ABC=90°,
AB⊥BC,
∵EF⊥BC,
∴AB∥EF,
∵OD⊥AB,
∴OD⊥EF,
∵OD是半径,
∴EF为⊙O的切线.

(1)证明:连接AD,
∵AB=AC,D为BC中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)证明:连接OD交AB于M,
∵D为弧AB中点,OD为半径,
∴OD⊥AB,
∵AC为直径,
∴∠ABC=90°,
AB⊥BC,
∵EF⊥BC,
∴AB∥EF,
∵OD⊥AB,
∴OD⊥EF,
∵OD是半径,
∴EF为⊙O的切线.
点评:本题考查了垂径定理、圆周角定理、等腰三角形的判定等知识的,注意:等腰三角形的三线合一定理,经过半径的外端且垂直于这条半径的直线是圆的切线.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 (2012•历下区二模)小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为( )
(2012•历下区二模)小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为( ) (2012•历下区二模)如图1,在直角梯形ABCD中,动点P从点B出发,沿BC→CD运动至点D停止.设点P运动的路程为x,△APB的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
(2012•历下区二模)如图1,在直角梯形ABCD中,动点P从点B出发,沿BC→CD运动至点D停止.设点P运动的路程为x,△APB的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )