题目内容
已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表:
| 甲 | 乙 | |
| 维生素A(单位/千克) | 300 | 500 |
| 维生素B(单位/千克) | 700 | 100 |
| 成本(元/千克) | 5 | 4 |
(1)求x的取值范围;
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价.
解:(1)根据题意得,
 ,
,
解得30≤x≤50;
(2)∵x+y=100,
∴y=100-x,
设混合食品的成本为W,则w=5x+4y=x+400,
∵W随x的增大而增大,
∴当x=30时,y=70,则w最小=430,
这时最低成本价为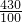 =4.3(元/千克),
=4.3(元/千克),
答:当x=30时,y=70,则w最小=430元时,这时最低成本价为4.3(元/千克).
分析:(1)根据甲、乙混合食品中要求维生素A不低于40000单位,B不低于28000单位列出不等式组解答即可;
(2)利用函数的性质,根据自变量的取值范围,找出函数的最小值即可解答.
点评:此题主要考查一次函数在实际问题中的嘴直问题以及一次不等式的实际应用,属于基础题型.
 ,
,解得30≤x≤50;
(2)∵x+y=100,
∴y=100-x,
设混合食品的成本为W,则w=5x+4y=x+400,
∵W随x的增大而增大,
∴当x=30时,y=70,则w最小=430,
这时最低成本价为
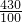 =4.3(元/千克),
=4.3(元/千克),答:当x=30时,y=70,则w最小=430元时,这时最低成本价为4.3(元/千克).
分析:(1)根据甲、乙混合食品中要求维生素A不低于40000单位,B不低于28000单位列出不等式组解答即可;
(2)利用函数的性质,根据自变量的取值范围,找出函数的最小值即可解答.
点评:此题主要考查一次函数在实际问题中的嘴直问题以及一次不等式的实际应用,属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表:
现将两种食物混合成100千克的混合食品.设混合食品中甲、乙食物含量分别为x(千克)和y(千克),如果混合食品中要求维生素A不低于40000单位,B不低于28000单位.
(1)求x的取值范围;
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价.
| 甲 | 乙 | |
| 维生素A(单位/千克) | 300 | 500 |
| 维生素B(单位/千克) | 700 | 100 |
| 成本(元/千克) | 5 | 4 |
(1)求x的取值范围;
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价.
已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表:
| | 甲 | 乙 |
| 维生素A(单位/千克) | 300 | 500 |
| 维生素B(单位/千克) | 700 | 100 |
| 成本(元/千克) | 5 | 4 |
(1)求x的取值范围
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价
已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表:
|
|
甲 |
乙 |
|
维生素A(单位/千克) |
300 |
500 |
|
维生素B(单位/千克) |
700 |
100 |
|
成本(元/千克) |
5 |
4 |
现将两种食物混合成100千克的混合食品。设混合食品中甲、乙食物含量分别为x(千克)和y(千克),如果混合食品中要求维生素A不低于40000单位,B不低于28000单位
(1)求x的取值范围
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价
已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表:
现将两种食物混合成100千克的混合食品.设混合食品中甲、乙食物含量分别为x(千克)和y(千克),如果混合食品中要求维生素A不低于40000单位,B不低于28000单位.
(1)求x的取值范围;
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价.
| 甲 | 乙 | |
| 维生素A(单位/千克) | 300 | 500 |
| 维生素B(单位/千克) | 700 | 100 |
| 成本(元/千克) | 5 | 4 |
(1)求x的取值范围;
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价.