��Ŀ����
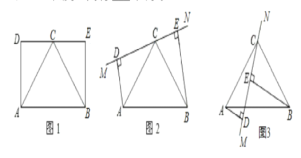
����Ŀ����Rt��ABC�У���BAC=90�㣬AD��BC�ڵ�D����O��AC����һ�㣬����BO����AD�ڵ�F��OE��OB��BC�ڵ�E��
��1����ͼ1����OΪ��AC�е㣬![]() ʱ����
ʱ����![]() ��ֵ.С��������ģ���O����OH��AB��BC�ڵ�H����֤��AOF�ס�HOE����������𰸣�����ֱ��д����
��ֵ.С��������ģ���O����OH��AB��BC�ڵ�H����֤��AOF�ס�HOE����������𰸣�����ֱ��д����![]() ��
��
��2����ͼ2����OΪ��AC�е㣬![]() ʱ�������
ʱ�������![]() ��ֵ,��˵�����ɣ�
��ֵ,��˵�����ɣ�
��3����ͼ3����![]() ,
,![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() ��ֵ��
��ֵ��

���𰸡�(1)2;(2)![]() ;(3)
;(3) ![]() .
.
��������
��1����֤����BAF=��C����ABF=��COE���ɣ���OH��AC����BC��H����֤����OEH�͡�OFA���ƣ�����֤����ABF�ס�HOE���������������εĶ�Ӧ�ߵı���ȣ����ɵó������ֵ��
��2��ͬ��1���ķ����ó�![]() ���������ɵó����ۣ�
���������ɵó����ۣ�
��3��ͬ��1���ķ����ó�![]() ���������ɵó����ۣ�
���������ɵó����ۣ�
��1��֤������AD��BC��
���DAC+��C=90�㣮
�ߡ�BAC=90�㣬
���BAF=��C��
��OE��OB��
���BOA+��COE=90�㣬
�ߡ�BOA+��ABF=90�㣬
���ABF=��COE��
��O��AC���߽�BC��H����OH��AB��
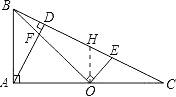
�ߡ�ABF=��COE����BAF=��C��
���AFB=��OEC��
���AFO=��HEO��
����BAF=��C��
���FAO=��EHO��
���OEH�ס�OFA��
��![]()
�֡�OΪAC���е㣬OH��AB��
��OHΪ��ABC����λ�ߣ�
��OH=![]() AB��OA=OC=
AB��OA=OC=![]() AC��
AC��
��![]() ��2��
��2��
��![]() ��
��
��![]() ��
��
��2��ͬ��1�������ã�![]() ��
��
���֡�OΪAC���е㣬OH��AB��
��OHΪ��ABC����λ�ߣ�
��OH=![]() AB��OA=OC=
AB��OA=OC=![]() AC��
AC��
��![]() ��
��
��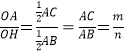 ��
��
��![]() ��
��
��3��ͬ��1�������ã�![]() ��
��
��OH��AB��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��

 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�