题目内容
设a,b是方程x2+x-2009=0的两个实数根,则a2+2a+b的值为
| A.2006 | B.2007 | C.2008 | D.2009 |
C
分析:由于a2+2a+b=(a2+a)+(a+b),故根据方程的解的意义,求得(a2+a)的值,由根与系数的关系得到(a+b)的值,即可求解.
解答:解:∵a是方程x2+x-2009=0的根,
∴a2+a=2009;
由根与系数的关系得:a+b=-1,
∴a2+2a+b=(a2+a)+(a+b)=2009-1=2008.
故选C.
解答:解:∵a是方程x2+x-2009=0的根,
∴a2+a=2009;
由根与系数的关系得:a+b=-1,
∴a2+2a+b=(a2+a)+(a+b)=2009-1=2008.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
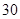 场,共有 个队参加比赛。
场,共有 个队参加比赛。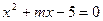 的一个根,求m的值及方程的另一根x2
的一个根,求m的值及方程的另一根x2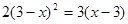 (2)
(2) 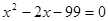
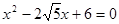 (4)
(4)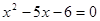
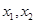 是方程
是方程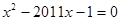 的两根,则
的两根,则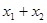 =________________;
=________________;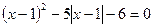
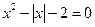 ;
;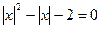 。令
。令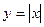 ,原方程化成
,原方程化成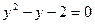

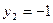
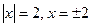 ;当
;当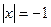
 时(不合题意,舍去)
时(不合题意,舍去) 

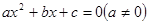 中,若有
中,若有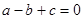 ,则方程必有一根为( )。
,则方程必有一根为( )。