جâؤ؟ؤعبف
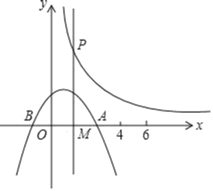
،¾جâؤ؟،؟ؤ³²ْئ·أ؟¼³ة±¾10شھ£¬تشدْ½×¶خأ؟¼²ْئ·µؤدْتغ¼غx£¨شھ£©سë²ْئ·µؤبصدْتغء؟y£¨¼£©ض®¼نµؤ¹طدµبçدآ±ي£؛
![]()
زرضھبصدْتغء؟yتاتغ¼غxµؤز»´خ؛¯ت£®
£¨1£©ض±½سذ´³ِبصدْتغء؟y£¨¼£©سëدْتغ¼غx£¨شھ£©µؤ؛¯ت¹طدµت½£»
£¨2£©زھت¹أ؟بصµؤدْتغہûبَ×î´َ£¬أ؟¼²ْئ·µؤتغ¼غس¦¶¨خھ¶àةظشھ£؟´ثت±µؤبصدْتغہûبَتا¶àةظ£؟
£¨3£©بôبصدْتغہûبَ²»µحسع125شھ£¬اëض±½سذ´³ِتغ¼غµؤب،ضµ·¶خ§£®
،¾´ً°¸،؟£¨1£©![]() £»£¨2£©²ْئ·µؤدْتغ¼غس¦¶¨خھ 25 شھ£¬ ´ثت±أ؟بصµؤدْتغہûبَ×î´َخھ 225 شھ£»£¨3£©
£»£¨2£©²ْئ·µؤدْتغ¼غس¦¶¨خھ 25 شھ£¬ ´ثت±أ؟بصµؤدْتغہûبَ×î´َخھ 225 شھ£»£¨3£©![]() .
.
،¾½âخِ،؟
£¨1£© زٍخھبصدْتغء؟![]() تادْتغ¼غ
تادْتغ¼غ![]() µؤز»´خ؛¯ت£¬ ةè
µؤز»´خ؛¯ت£¬ ةè![]() £¬´ْبë¶شس¦تضµاَ³ِ؛¯ت½âخِت½¼´؟ة£»
£¬´ْبë¶شس¦تضµاَ³ِ؛¯ت½âخِت½¼´؟ة£»
£¨2£© ہûسأدْتغہûبَ![]() ز»¼ہûبَ
ز»¼ہûبَ![]() دْتغ¼ت£¬ ز»¼ہûبَ
دْتغ¼ت£¬ ز»¼ہûبَ![]() دْتغ¼غ
دْتغ¼غ![]() ³ة±¾£¬ بصدْتغء؟
³ة±¾£¬ بصدْتغء؟![]() تادْتغ¼غ
تادْتغ¼غ![]() µؤز»´خ؛¯ت£¬ اَµأہûبَ
µؤز»´خ؛¯ت£¬ اَµأہûبَ![]() خھ¶´خ؛¯ت£¬ شثسأ¶´خ؛¯تµؤذشضت£¬ ؟ةاَ×î´َہûبَ£»
خھ¶´خ؛¯ت£¬ شثسأ¶´خ؛¯تµؤذشضت£¬ ؟ةاَ×î´َہûبَ£»
£¨3£©ہûسأ،°بصدْتغہûبَ²»µحسع،±؟ةµأ![]() £¬´س¶ّ؟ةاَ
£¬´س¶ّ؟ةاَ![]() µؤ·¶خ§ £®
µؤ·¶خ§ £®
½â£؛ £¨1£© ةè´ثز»´خ؛¯ت¹طدµت½خھ![]() £¬
£¬
شٍ![]() £¬
£¬
½âµأ![]() £¬
£¬![]()
¹تز»´خ؛¯تµؤ¹طدµت½خھ![]() £®
£®
£¨2£© ةèثù»ٌہûبَخھ![]() شھ£¬
شھ£¬
شٍ![]()
ثùزش²ْئ·µؤدْتغ¼غس¦¶¨خھ 25 شھ£¬ ´ثت±أ؟بصµؤدْتغہûبَخھ 225 شھ£»
£¨3£©¸ù¾فجâزâ؟ةµأ![]() £¬
£¬
½âµأ£؛![]() £®
£®
´ً£؛تغ¼غµؤب،ضµ·¶خ§خھ£؛![]() .
.

 أûذ£؟خجأدµءذ´ً°¸
أûذ£؟خجأدµءذ´ً°¸