题目内容
23、已知：如图，在平行四边形ABCD中，点E、F分别在边BC和AD上，且∠BAE=∠DCF．求证：四边形AECF是平行四边形．
分析：平行四边形的对边平行，对角相等，根据此可求出四边形AECF另一组对边平行，根据两组对边平行的四边形是平行四边形，从而可证明．
解答：证明：在平行四边形ABCD中，
∵∠B=∠D，∠BAE=∠DCF，
∴∠AEB=∠CFD．（1分）
∵AD∥BC，
∴∠AEB=∠EAD．（2分）
∴∠CFD=∠EAD．（1分）
∴AE∥CF．（1分）
∵AF∥CE，
∴四边形AECF是平行四边形．（2分）
∵∠B=∠D，∠BAE=∠DCF，
∴∠AEB=∠CFD．（1分）
∵AD∥BC，
∴∠AEB=∠EAD．（2分）
∴∠CFD=∠EAD．（1分）
∴AE∥CF．（1分）
∵AF∥CE，
∴四边形AECF是平行四边形．（2分）
点评：本题考查平行四边形的性质定理和判定定理，以及平行线的判定定理，本题用两组对边平行的四边形是平行四边形进行证明．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
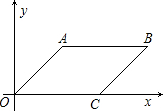如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，