题目内容
如图,已知点D在AC上,△ABC和△ADE都是等腰直角三角形,点M为EC的中点.
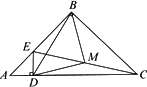
(1)求证:△BMD为等腰直角三角形
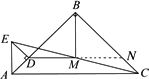
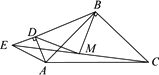
(2)将△ADE绕点A逆时针旋转45°,如图,(1)中的“△BMD为等腰直角三角形”是否仍然成立?请说明理由.
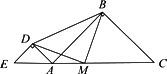
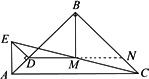
(3)将△ADE绕点A逆时针旋转135°,如图,(1)中的“△BMD为等腰直角三角形”成立吗?(不用说明理由).
(4)我们是否可以猜想,将△ADE绕点A任意旋转一定的角度,如图,(1)中的“△BMD为等腰直角三角形”均成立?(不用说明理由).
答案:
解析:
解析:
(1)证明:
∵点M是Rt△BEC的斜边EC的中点,
∴BM=![]() EC=MC,
EC=MC,
∴∠MBC=∠MCB.
∴∠BME=2∠BCM.
同理可证:DM=![]() EC=MC,
EC=MC,
∠EMD=2∠MCD. 1分
∴∠BMD=2∠BCA=90°,
∴BM=DM.
∴△BMD是等腰直角三角形. 2分
(2)(1)中的结论仍然成立. 3分
延长DM与BC交于点N
∵DE⊥AB
CB⊥AB,
∴∠EDB=∠CBD=90°
∴DE∥BC.
∴∠DEM=∠MCN.
又∵∠EMD=∠NMC,EM=MC
∴△EDM≌△MNC 4分
∴DM=MN.
DE=NC=AD.
又AB=BC,
∴AB-AD=BC-CN
∴BD=BN.
∴BM⊥DM.
即∠BMD=90°.
∵∠ABC=90°,
∴BM=![]() DN=DM.
DN=DM.
∴△BMD是等腰直角三角形. 5分

(3)(1)中的结论成立. 6分
(4)(1)中的结论成立. 7分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
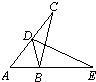 25、如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=5:3,则∠DBC=( )
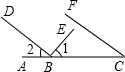
25、如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=5:3,则∠DBC=( )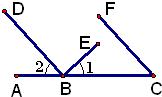 29、如图,已知点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?说明理由.
29、如图,已知点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?说明理由.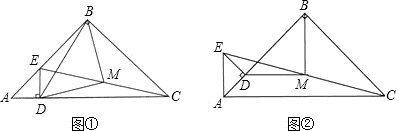
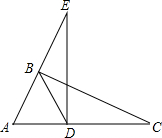 如图,已知点D在AC上,点B在AE上,△ABC≌△ADE,且∠A=∠ABD.若∠A:∠C=5:3,则∠BDE等于( )
如图,已知点D在AC上,点B在AE上,△ABC≌△ADE,且∠A=∠ABD.若∠A:∠C=5:3,则∠BDE等于( )