题目内容
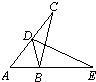 25、如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=5:3,则∠DBC=( )
25、如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=5:3,则∠DBC=( )分析:根据全等三角形的性质,∠BDE=∠A=∠BDA,∠E=∠C,又∠ABD=∠BDE+∠E,∠A:∠C=5:3,在△ABD中根据内角和定理求解.
解答:解:由△ABC≌△DBE,
∴∠BDE=∠A=∠BDA,∠E=∠C,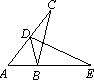
∵∠A:∠C=5:3,
∴∠A:∠BDA:∠BDE:∠E=5:5:5:3,
又∠A+∠BDA+∠BDE+∠E=180°,
∴∠C=∠E=30°,∠BDE=∠A=∠BDA=50°,∠CDE=∠A+∠E=50°+30°=80°,
∴∠DBC=180°-∠C-∠CDE-∠BDE=180°-30°-80°-50°=20°.
故选C.
∴∠BDE=∠A=∠BDA,∠E=∠C,

∵∠A:∠C=5:3,
∴∠A:∠BDA:∠BDE:∠E=5:5:5:3,
又∠A+∠BDA+∠BDE+∠E=180°,
∴∠C=∠E=30°,∠BDE=∠A=∠BDA=50°,∠CDE=∠A+∠E=50°+30°=80°,
∴∠DBC=180°-∠C-∠CDE-∠BDE=180°-30°-80°-50°=20°.
故选C.
点评:本题考查全等三角形的性质和三角形的内角和定理,难度也比较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
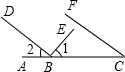
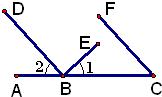 29、如图,已知点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?说明理由.
29、如图,已知点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?说明理由.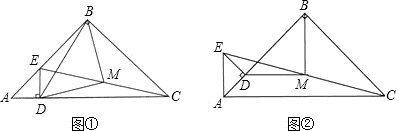
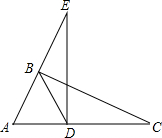 如图,已知点D在AC上,点B在AE上,△ABC≌△ADE,且∠A=∠ABD.若∠A:∠C=5:3,则∠BDE等于( )
如图,已知点D在AC上,点B在AE上,△ABC≌△ADE,且∠A=∠ABD.若∠A:∠C=5:3,则∠BDE等于( )