题目内容
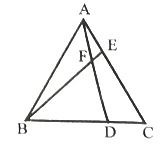
【题目】定义:如(图1),点![]() 把线段
把线段![]() 分割成
分割成![]() 和
和![]() ,若以
,若以![]() 为边的三角形是一个直角三角形,则称点
为边的三角形是一个直角三角形,则称点![]() 是线段
是线段![]() 的勾股分割点.
的勾股分割点.
(1)已知点![]() 是线段
是线段![]() 的勾股分割点,若
的勾股分割点,若![]() ,求
,求![]() 的长;
的长;
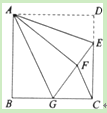
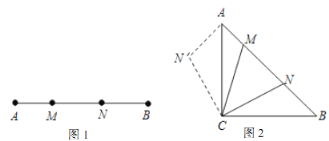
(2)如(图2),在等腰直角![]() 中,
中, ![]() ,点
,点![]() 为边
为边![]() 上两点,满足
上两点,满足![]() ,求证:点
,求证:点![]() 是线段
是线段![]() 的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把
的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 试一试.请根据陈老师的提示完成第(2)小题的证明过程.
试一试.请根据陈老师的提示完成第(2)小题的证明过程.
【答案】(1)BN=![]() 或
或![]() ;(2)见解析
;(2)见解析
【解析】
(1)分当MN为最大线段时和当BN为最大线段时,两种情况利用勾股定理即可解决问题;
(2)先证明△MCN≌△MCN′,得MN′=MN,由勾股定理得AN′2+AM2=MN′2,即可解答;
(1)解:①当MN为最大线段时,
∵点 M , N是线段AB的勾股分割点,
∴BN=![]() =
=![]() =
=![]() ;
;
②当BN为最大线段时,
∵点M , N是线段AB的勾股分割点,
∴BN=![]() =
=![]() ,
,
综上所述:BN=![]() 或
或![]() ;
;
(2)①证明:如图,连接MN′

∵∠ACB=90°,∠MCN=45°,∴∠BCN+∠ACM=45°,
∵∠AC N′=∠BCN,
∴∠MC N′=∠ACN′+∠ACM=∠BCN+∠ACM=45°=∠MCN,
在△MCN和△MCN′中,

∴△MCN≌△MC N′
∴M N′=MN
∵∠CAN′=∠CAB=45°
∴∠MAN ′=90,
AN′2+AM2=MN′2
即BN 2+AM 2=MN 2,
∴点M , N是线段AB的勾股分割点

练习册系列答案
相关题目