题目内容
如图,在菱形ABCD中,∠A=60°,AB=4,E是边AB上一动点,过点E作EF⊥AB交AD的延长线于点F,交BD于点M.
(1)请判断△DMF的形状,并说明理由.
(2)设EB=x,△DMF的面积为y,求y与x之间的函数关系式.并写出x的取值范围.
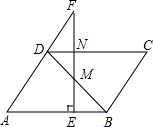
(1)请判断△DMF的形状,并说明理由.
(2)设EB=x,△DMF的面积为y,求y与x之间的函数关系式.并写出x的取值范围.

(1)△DMF是等腰三角形.理由如下:(2分)
∵四边形ABCD是菱形
∴AB=AD,
∵∠A=60°,
∴∠ABD=60°,
∵EF⊥AB,
∴∠F=30°,∠DMF=∠EMB=30°,
∴∠F=∠DMF,
∴DM=DF,
∴△DMF是等腰三角形.
(2)EB=x,则AE=4-x,由tan60°=
,则EF=
(4-x),EN=2
,
∴NF=EF-EN=
(2-x),FM=2
(2-x).
∵MN=NF=
(2-x),
∴DN=MNtan30°=2-x,
∴y=
FM•DN=
(2-x)×2
(2-x)=
(2-x)2,(0≤x<2).

∵四边形ABCD是菱形
∴AB=AD,
∵∠A=60°,
∴∠ABD=60°,
∵EF⊥AB,
∴∠F=30°,∠DMF=∠EMB=30°,
∴∠F=∠DMF,
∴DM=DF,
∴△DMF是等腰三角形.
(2)EB=x,则AE=4-x,由tan60°=
| EF |
| AE |
| 3 |
| 3 |
∴NF=EF-EN=
| 3 |
| 3 |
∵MN=NF=
| 3 |
∴DN=MNtan30°=2-x,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |


练习册系列答案
相关题目