题目内容
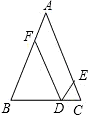如图，从等腰△ABC底边BC上任意一点D分别作两腰的平行线DE、DF，分别交AC、AB于点E、F，则?AFDE的周长等于这个等腰三角形的
- A.周长
- B.周长的一半
- C.一条腰长的2倍
- D.一条腰长
C
分析：根据等腰三角形的性质可得到两底角相等，再根据平行四边形的性质可推出DE=EC，根据平行四边形的周长公式不难求解．
解答：∵AB=AC，
∴∠B=∠C，
∵DE∥AB，
∴∠B=∠EDC，
∴DE=EC，
∵四边形AEDF是平行四边形，
∴DE=AF，
∴AF=CE，
∴?AEDF的周长=2（AF+AE）=2AC．
故选C．
点评：此题主要考查等腰三角形的性质及平行四边形的性质的综合运用．
分析：根据等腰三角形的性质可得到两底角相等，再根据平行四边形的性质可推出DE=EC，根据平行四边形的周长公式不难求解．
解答：∵AB=AC，
∴∠B=∠C，
∵DE∥AB，
∴∠B=∠EDC，
∴DE=EC，
∵四边形AEDF是平行四边形，
∴DE=AF，
∴AF=CE，
∴?AEDF的周长=2（AF+AE）=2AC．
故选C．
点评：此题主要考查等腰三角形的性质及平行四边形的性质的综合运用．
练习册系列答案
名校课堂系列答案
相关题目
运动到点A时，点Q、p停止运动，设它们运动的时间为x cm．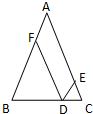
3、如图，从等腰△ABC底边BC上任意一点D分别作两腰的平行线DE、DF，分别交AC、AB于点E、F，则?AFDE的周长等于这个等腰三角形的（ ）
