题目内容
(2007•白银)如图,秋千拉绳的长OB=4米,静止时,踏板到地面的距离BE=0.6米(踏板厚度忽略不计).小强荡该秋千时,当秋千拉绳OB运动到最高处OA时,拉绳OA与铅垂线OE的夹角为60°,试求:(1)当秋千拉绳OB运动到最高处OA时,踏板离地面的高度AD是多少米?
(2)秋千荡回到OC(最高处)时,小强荡该秋千的“宽度”AC是多少米?(结果保留根号)

【答案】分析:(1)在直角△AFO中,根据三角函数就可以求出OF,进而求得BF,求出AD.
(2)在Rt△AFO中根据三角函数可以求出AF,则AC=2AF.
解答:解:(1)在Rt△AFO中
∵∠OAF=30°
∴OF= OA=2.
OA=2.
∴EF=OB+BE-OF=4+0.6-2=2.6.
∴AD=EF=2.6(米).
(2)∵AF=OA×sin60°=
又OB⊥AC,
∴AC=2AF=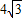 (米).
(米).
点评:本题考查了直角三角形的应用,三角函数的性质.属于常规题.
(2)在Rt△AFO中根据三角函数可以求出AF,则AC=2AF.
解答:解:(1)在Rt△AFO中
∵∠OAF=30°
∴OF=
 OA=2.
OA=2.∴EF=OB+BE-OF=4+0.6-2=2.6.
∴AD=EF=2.6(米).
(2)∵AF=OA×sin60°=

又OB⊥AC,
∴AC=2AF=
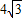 (米).
(米).点评:本题考查了直角三角形的应用,三角函数的性质.属于常规题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目