题目内容
【题目】如图,等腰直角![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,连接
,连接![]()
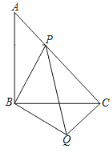
(1)求![]() 的度数;
的度数;
(2)当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)90°;(2)![]()
【解析】
(1)根据余角的性质得到∠ABP=∠CBQ,根据全等三角形的性质得到∠BCQ=∠A,根据等腰直角三角形的性质即可得到结论;
(2)过P作PD⊥AB于D,得到△ADP是等腰直角三角形,于是得到AD=PD=![]() AP=1,根据勾股定理即可得到结论.
AP=1,根据勾股定理即可得到结论.
解:(1)∵∠ABC=90°,∠PBQ=90°,
∴∠ABP=90°-∠CBP,∠CBQ=90°-∠CBP,
∴∠ABP=∠CBQ,
∵AB=BC,BP=BQ,
∴△ABP≌△CBQ(SAS),
∴∠BCQ=∠A,
∵△ABC是等腰直角三角形,
∴∠A=∠ACB=45°,
∴∠BCQ=45°,
∴∠PCQ=45°+45°=90°;
(2)过P作PD⊥AB于D,
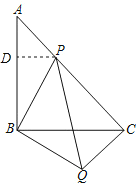
则△ADP是等腰直角三角形,
∴AD=PD=![]() AP=1,
AP=1,
∵AB=4,
∴BD=3,
∴PB=![]() .
.

练习册系列答案
相关题目