Question

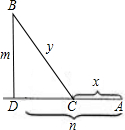
如图，城市A位于一条铁路线上，而附近的一小镇B需从A市购进大量生活、生产用品，如果铁路运费是公路运费的一半．问该如何从B修筑一条公路到铁路边，使从A到B的运费最低？

Answer 1

设AC=x千米，BC=y千米，AD=n千米，BD=m千米，铁路每千米的运费为a元，则公路每千米的运费为2a元，
则从A到B得运费s=a（n-

y2-m2

）+2ay①，即an-s+2ay=a

y2-m2

②，
两边平方整理得：3a²y²+4a（an-s）y+（an-s）²+a²m²=0，
可看作关于y的一元二次方程，△=[4a（an-s）]²-4×3a²[（an-s）²+a²m²]≥0，
即（an-s）²≥3a²m²，s-an≥

3

am，
从而可得s≥an+

3

am，故最小值为an+

3

am．
将s的值代入②可得an-（an+

3

am）+2ay=a

y2-m2

，
移项后可得：(

3

ay-2am)2=0，故

3

ay=2am，
解得：y=

2 3 m

3

，
从而可得x=n-

y2-m2

=n-

3

3

m．
答：修一条公路，使得铁路与公路的交接点C距离A的距离为n-

3

3

m，此时的运费最低，为an+

3

am．