Question

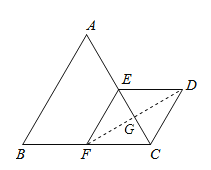
【题目】如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点．

（1）求证：四边形EFCD是菱形；

（2）如果AB=8，求D、F两点间的距离．

Answer 1

【答案】（1）证明见解析；（2）

【解析】试题分析：

（1）由△ABC是等边三角形，点E、F分别为AC、BC的中点可证得：EF=EC=FC；由△DEC是等边三角形可得：DE=DC=EC，从而可得EF=FC=CD=DE，由此可得：四边形EFCD是菱形；

（2）连接DF交AC于点G，由已知易证EF=EC=4，再由菱形的对角线互相垂直平分，可得EG=2，再由勾股定理可得：FG=，从而可得DF=.

试题解析：

（1）∵△ABC与△CDE都是等边三角形

∴AB=AC=BC，ED=DC=EC

∵点E、F分别为AC、BC的中点

∴EF=AB，EC=AC，FC=BC

∴EF=EC=FC

∴EF=FC=ED=DC，

∴四边形EFCD是菱形．

（2）连接DF，与EC相交于点G，

∵四边形EFCD是菱形，

∴DF⊥EC，垂足为G ，EG=EC，

∴∴∠EGF=90°，

又∵AB=8， EF=AB，EC=AC，

∴EF=4，EC=4，EG=2，

∴GF=，

∴DF=2GF=.