题目内容
【题目】The coordinates of the three points A.B.C on the plane are (﹣5,﹣5),(﹣2,﹣1)and(﹣1,﹣2)respectively,the triangle ABC is( ) (英汉小词典:right直角的;isosceles等腰的;equilateral等边的;obtuse钝角的)
A.a right trisngle
B.an isosceles triangle
C.an equilateral triangle
D.an obtuse triangle
【答案】B
【解析】解答:如图过B作Y轴的平行线,过A作X轴的平行线,两线交于H,由勾股定理得:AB2=[(﹣2)﹣(﹣5)]2+[(﹣1)﹣(﹣5)]2, 即:AB2=25
同理:AC2=[(﹣1)﹣(﹣5)]2+[(﹣2)﹣(﹣5)]2,即:AC2=25,
BC2=[(﹣1)﹣(﹣2)]2+[(﹣1)﹣(﹣2)]2,BC2=2,
∴AB=AC.
故选B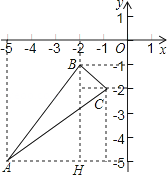
分析:过B作Y轴的平行线,过A作X轴的平行线,两线交于H,构造直角三角形,根据勾股定理求出AB的长,同理求出AC、BC的长,比较即可得出答案,本题主要考查了等腰三角形的判定,勾股定理的逆定理等知识点,解此题的关键是能根据点的坐标求出AB、BC、AC的长度
【考点精析】认真审题,首先需要了解等腰三角形的判定(如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等),还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形)的相关知识才是答题的关键.

练习册系列答案
相关题目