题目内容
已知:如图,在平面直角坐标系xOy中,AB∥x轴,点C是点B关于原点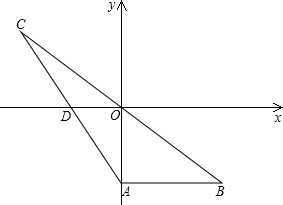 O的对称点,连接AC交x轴于点D,点A的坐标为(0,-3),sinB=
O的对称点,连接AC交x轴于点D,点A的坐标为(0,-3),sinB=| 3 | 5 |
(1)求B、C、D三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)设点E(8,n)在(2)中的抛物线上,请你在x轴上求一点F,使得△DEF是以DE为底边的等腰三角形.
分析:(1)本题需先根据题意得出OA、OB、AB的长,先求出B的坐标,再根据对称求出C、D两点的坐标即可.
(2)本题需先设出抛物线的解析式y=ax2+bx-3,然后列出方程组求出a、b的值,即可得出所求抛物线的解析式.
(3)本题需先求出E点的坐标,再设F点的坐标为F(m,0),根据DF=EF列出方程,解出m的值,即可求出F点的坐标.
(2)本题需先设出抛物线的解析式y=ax2+bx-3,然后列出方程组求出a、b的值,即可得出所求抛物线的解析式.
(3)本题需先求出E点的坐标,再设F点的坐标为F(m,0),根据DF=EF列出方程,解出m的值,即可求出F点的坐标.
解答: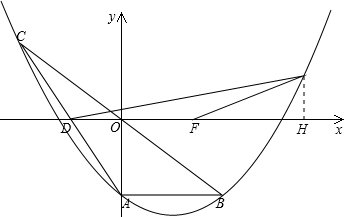 解:(1)∵点A的坐标为(0,-3),
解:(1)∵点A的坐标为(0,-3),
∴OA=3.
∵AB∥x轴,
∴∠OAB=90°.
∴sinB=
=
.
∴OB=5.
∴AB=4.
∴B点坐标为:B(4,-3).
∵点C是点B关于原点O的对称点,
∴C点坐标为:C(-4,3),且OC=OB.
∴OD=
AB=2.
∴D点坐标为:D(-2,0);
(2)设过A,B,C三点的抛物线的解析式为y=ax2+bx-3,
∴
,
解得
,
所求抛物线的解析式为y=
x2-
x-3;
(3)当x=8时,y=
×64-
×8-3=3.
∴E点坐标为:E(8,3).
设F点的坐标为F(m,0),
∴DF=m+2.
过点E作EH⊥x轴于H,
∴EF2=EH2+FH2=32+(8-m)2.
∵DF=EF,
∴(m+2)2=32+(8-m)2.
解得
.
F点的坐标为(
,0)
 解:(1)∵点A的坐标为(0,-3),
解:(1)∵点A的坐标为(0,-3),∴OA=3.
∵AB∥x轴,
∴∠OAB=90°.
∴sinB=
| OA |
| OB |
| 3 |
| 5 |
∴OB=5.
∴AB=4.
∴B点坐标为:B(4,-3).
∵点C是点B关于原点O的对称点,
∴C点坐标为:C(-4,3),且OC=OB.
∴OD=
| 1 |
| 2 |
∴D点坐标为:D(-2,0);
(2)设过A,B,C三点的抛物线的解析式为y=ax2+bx-3,
∴
|
解得
|
所求抛物线的解析式为y=
| 3 |
| 16 |
| 3 |
| 4 |
(3)当x=8时,y=
| 3 |
| 16 |
| 3 |
| 4 |
∴E点坐标为:E(8,3).
设F点的坐标为F(m,0),
∴DF=m+2.
过点E作EH⊥x轴于H,
∴EF2=EH2+FH2=32+(8-m)2.
∵DF=EF,
∴(m+2)2=32+(8-m)2.
解得
| 69 |
| 20 |
F点的坐标为(
| 69 |
| 20 |
点评:本题主要考查了二次函数的综合应用,在解题时要结合图形列出方程,求出点的坐标是本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).