题目内容
如图,把等腰直角三角形ABC沿直线BC方向向右平移到△DEF的位置,AC交DE于点O,连接AD,如果AB=2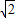 ,BF=6,那么△AOD的面积为 .
,BF=6,那么△AOD的面积为 .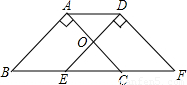
【答案】分析:先由△ABC是等腰直角三角形,得出AC=AB=2 ,BC=4,∠BAC=90°,∠B=45°,再根据平移的性质得出AO=
,BC=4,∠BAC=90°,∠B=45°,再根据平移的性质得出AO=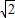 ,并且证明出△AOD是等腰直角三角形,然后根据三角形的面积公式即可求解.
,并且证明出△AOD是等腰直角三角形,然后根据三角形的面积公式即可求解.
解答:解:∵△ABC是等腰直角三角形,
∴AC=AB=2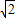 ,BC=
,BC= AB=4,∠BAC=90°,∠B=45°.
AB=4,∠BAC=90°,∠B=45°.
∵把等腰直角三角形ABC沿直线BC方向向右平移到△DEF的位置,AB=2 ,BF=6,
,BF=6,
∴四边形ABDE是平行四边形,BC=EF=4,BE=CF=BF-EF=6-4=2,
∴CE=BC-BE=4-2=2,∠AOD=90°,∠DAO=180°-∠BAC-∠B=45°,
∴CE=EB=2,OE是△ABC的中位线,△AOD是等腰直角三角形,
∴AO= AC=
AC= ,
,
∴△AOD的面积= ×OA×OD=
×OA×OD= ×
× ×
× =1.
=1.
故答案为1.
点评:本题主要考查了等腰直角三角形的性质,平移的性质,三角形的面积,综合性较强,难度适中,得出△AOD是等腰直角三角形是解题的关键.
 ,BC=4,∠BAC=90°,∠B=45°,再根据平移的性质得出AO=
,BC=4,∠BAC=90°,∠B=45°,再根据平移的性质得出AO=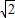 ,并且证明出△AOD是等腰直角三角形,然后根据三角形的面积公式即可求解.
,并且证明出△AOD是等腰直角三角形,然后根据三角形的面积公式即可求解.解答:解:∵△ABC是等腰直角三角形,
∴AC=AB=2
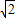 ,BC=
,BC= AB=4,∠BAC=90°,∠B=45°.
AB=4,∠BAC=90°,∠B=45°.∵把等腰直角三角形ABC沿直线BC方向向右平移到△DEF的位置,AB=2
 ,BF=6,
,BF=6,∴四边形ABDE是平行四边形,BC=EF=4,BE=CF=BF-EF=6-4=2,
∴CE=BC-BE=4-2=2,∠AOD=90°,∠DAO=180°-∠BAC-∠B=45°,
∴CE=EB=2,OE是△ABC的中位线,△AOD是等腰直角三角形,
∴AO=
 AC=
AC= ,
,∴△AOD的面积=
 ×OA×OD=
×OA×OD= ×
× ×
× =1.
=1.故答案为1.
点评:本题主要考查了等腰直角三角形的性质,平移的性质,三角形的面积,综合性较强,难度适中,得出△AOD是等腰直角三角形是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
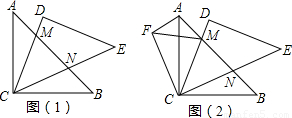
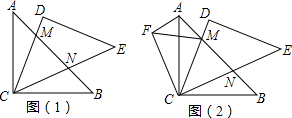 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由. 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.