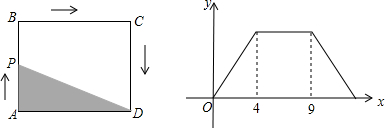题目内容
动点P从长方形的顶点A出发,以1cm/s的速度,沿边按箭头方向运动,到达点D停止.△ADP的面积y(cm2)与运动时间x(S)之间的函数图象如图所示.(规定:点P在点A、D时,y=0)
(1)根据图象和点P的位置填空:AB=______cm,BC=______cm.
(2)当点P在边______上运动时,y的值保持不变.
(3)直接写出y与x之间的函数关系式及相应的x的取值范围.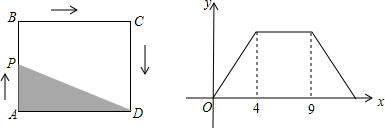
解:(1)由图形可知,点P在AB上运动的时间为4秒,在BC上运动的时间为9-4=5秒,
∵点P的速度是1cm/s,
∴AB=1×4=4cm,
BC=1×5=5cm;
(2)点P在BC上时,P到AD的距离不变,始终等于AB的长度,
所以,当点P在边BC上运动时,y的值保持不变;
(3)点P在AB上时,y= ×5x=
×5x= x,(0≤x≤4),
x,(0≤x≤4),
在BC上时,y= ×4×5=10,(4<x<9),
×4×5=10,(4<x<9),
在CD上时,y= ×(4+5+4-x)×5=
×(4+5+4-x)×5= (13-x)=-
(13-x)=- x+
x+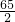 ,(9≤x≤13),
,(9≤x≤13),
所以,y与x之间的函数关系式为y=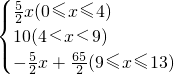 .
.
分析:(1)根据△ADP的底边AD不变,点P在AB边上运动时,面积随着点P的运动逐渐增大,在BC上运动时,根据矩形的性质,高等于AB的长度不变,面积不变,然后根据第二个图形得到在AB、BC上运动的时间,再利用路程=速度×时间解答;
(2)根据三角形的面积公式,在BC上运动时,底边与高都不变,所以,y值保持不变;
(3)分点P在AB上,在BC上,在CD上三种情况用x表示出点P到AD的距离,然后根据三角形的面积公式列式进行计算即可得解.
点评:本题考查了动点问题函数图象,根据点P在矩形的边上运动的情况,判断出点P到AD边的高的变化情况,得到面积的变化情况,从而得到点P在AB、BC边上运动的时间是解题的关键.
∵点P的速度是1cm/s,
∴AB=1×4=4cm,
BC=1×5=5cm;
(2)点P在BC上时,P到AD的距离不变,始终等于AB的长度,
所以,当点P在边BC上运动时,y的值保持不变;
(3)点P在AB上时,y=
 ×5x=
×5x= x,(0≤x≤4),
x,(0≤x≤4),在BC上时,y=
 ×4×5=10,(4<x<9),
×4×5=10,(4<x<9),在CD上时,y=
 ×(4+5+4-x)×5=
×(4+5+4-x)×5= (13-x)=-
(13-x)=- x+
x+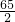 ,(9≤x≤13),
,(9≤x≤13),所以,y与x之间的函数关系式为y=
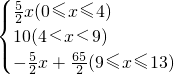 .
.分析:(1)根据△ADP的底边AD不变,点P在AB边上运动时,面积随着点P的运动逐渐增大,在BC上运动时,根据矩形的性质,高等于AB的长度不变,面积不变,然后根据第二个图形得到在AB、BC上运动的时间,再利用路程=速度×时间解答;
(2)根据三角形的面积公式,在BC上运动时,底边与高都不变,所以,y值保持不变;
(3)分点P在AB上,在BC上,在CD上三种情况用x表示出点P到AD的距离,然后根据三角形的面积公式列式进行计算即可得解.
点评:本题考查了动点问题函数图象,根据点P在矩形的边上运动的情况,判断出点P到AD边的高的变化情况,得到面积的变化情况,从而得到点P在AB、BC边上运动的时间是解题的关键.

练习册系列答案
相关题目