题目内容
如果有理数a、b、c满足，a+b+c=0，abc＞0，那么a、b、c中负数的个数是（ ）
| A．0 ； | B．1 ； | C．2 ； | D．3 ； |
C
分析：先根据abc＞0，结合有理数乘法法则，易知a、b、c中有2个负数或没有一个负数（都是正数），而都是正数，则a+b+c＞0，不符合a+b+c=0的要求，于是可得a、b、c中必有2个负数．
解答：解：∵abc＞0，
∴a、b、c中有2个负数或没有一个负数，
若没有一个负数，则a+b+c＞0，不符合a+b+c=0的要求，
故a、b、c中必有2个负数．
故选C．
解答：解：∵abc＞0，
∴a、b、c中有2个负数或没有一个负数，
若没有一个负数，则a+b+c＞0，不符合a+b+c=0的要求，
故a、b、c中必有2个负数．
故选C．
练习册系列答案
考前必练系列答案
相关题目
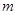是正整数，则
的值 （ ）
原数是200000 
原数是7580000000
原数是149000000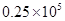 
原数是2500
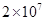
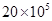
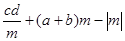的值为 _ * _ 。
（2）-（-2）×（-3） 
）
（
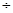） （4）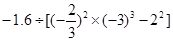
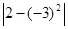
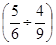×(-2)4