题目内容
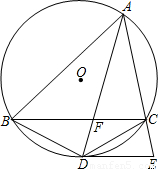
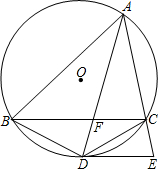 已知△ABC是圆O的内接三角形,∠BAC的平分线交BC于F交圆O于D,DE切圆O于D交AC的延长线于E,连BD,若BD=3
已知△ABC是圆O的内接三角形,∠BAC的平分线交BC于F交圆O于D,DE切圆O于D交AC的延长线于E,连BD,若BD=3| 2 |
分析:利用切线的性质以及圆周角、弦切角、弧之间的关系证明直线平行和三角形相似分别求出AB、AC、DE、EC的值,然后利用三角形相似求出FC,AF,DF的值,最后利用相交弦定理求出BF的值,从而求出BC的值.
解答:解:∵DE是圆O的切线,
∴∠CDE=∠CBD=∠DAE.
∴△ADE∽△DCE
∴
=
∴DE2=AE•EC
∴DE2=(AC+EC)EC
∵DE+EC=6
∴DE=6-EC
∴(6-EC)2=AC•EC+EC2
∵∠CBD=∠DAC,
∴∠CDE=∠DAC.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴∠CDE=∠BAD,BD=DC=3
.
∵∠BAD=∠BCD,
∴∠CDE=∠BCD.
∴BC∥DE.
∴△ABD∽△DCE,
∴
=
∴AB•EC=18
∵AB:AC=3:2
设AB=3x,AC=2x,EC=y,则有
解得:
∴AB=9,AC=6,EC=2
∴DE=4
∵BC∥DE.
∴△AFC∽△ADE
∴
=
=
∴
=
∴FC=3
可以证明△DFC∽△BFA
∴
=
∴
=
FA=
∴
=
∴AD=6
∴DF=
∵DF•AF=BF•FC
∴
×
=3BF
∴BF=
∴BC=
+3=
.
故BC的长为
.
∴∠CDE=∠CBD=∠DAE.
∴△ADE∽△DCE
∴
| DE |
| EC |
| AE |
| DE |
∴DE2=AE•EC
∴DE2=(AC+EC)EC
∵DE+EC=6
∴DE=6-EC
∴(6-EC)2=AC•EC+EC2
∵∠CBD=∠DAC,
∴∠CDE=∠DAC.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴∠CDE=∠BAD,BD=DC=3
| 2 |
∵∠BAD=∠BCD,
∴∠CDE=∠BCD.
∴BC∥DE.
∴△ABD∽△DCE,
∴
| AB |
| CD |
| BD |
| CE |
∴AB•EC=18
∵AB:AC=3:2
设AB=3x,AC=2x,EC=y,则有
|
解得:
|
∴AB=9,AC=6,EC=2
∴DE=4
∵BC∥DE.
∴△AFC∽△ADE
∴
| AC |
| AE |
| FC |
| DE |
| AF |
| AD |
∴
| 6 |
| 8 |
| FC |
| 4 |
∴FC=3
可以证明△DFC∽△BFA
∴
| DC |
| AB |
| FC |
| FA |
∴
3
| ||
| 9 |
| 3 |
| FA |
FA=
9
| ||
| 2 |
∴
| 3 |
| 4 |
| ||||
| AD |
∴AD=6
| 2 |
∴DF=
3
| ||
| 2 |
∵DF•AF=BF•FC
∴
3
| ||
| 2 |
9
| ||
| 2 |
∴BF=
| 9 |
| 2 |
∴BC=
| 9 |
| 2 |
| 15 |
| 2 |
故BC的长为
| 15 |
| 2 |
点评:本题是一道切线的性质运用的解答题,考查了切割线定理,相交弦定理以及相似三角形的判定及性质、平行线的判定.综合性较强,难度较大.

练习册系列答案
相关题目
 ,交AY于点D.
,交AY于点D.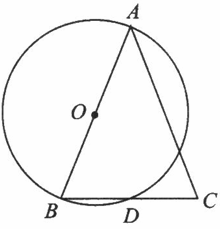
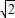 ,DE+EC=6,AB:AC=3:2,求BC的长.
,DE+EC=6,AB:AC=3:2,求BC的长.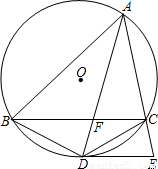
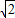 ,DE+EC=6,AB:AC=3:2,求BC的长.
,DE+EC=6,AB:AC=3:2,求BC的长.