题目内容
【题目】如图,正比例函数![]() 的图象过点
的图象过点![]() .直线
.直线![]() 沿y轴平行移动,与x轴,y轴分别交于点B,C,与直线OA交于点D.
沿y轴平行移动,与x轴,y轴分别交于点B,C,与直线OA交于点D.
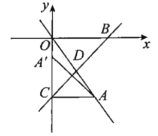
(1)若点D在线段OA上(含端点),求b的取值范围;
(2)当点A关于直线BC的对称点A恰好落在y轴上时,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将O点和A点的坐标分别代入y=x+b,即可求得b的值,从而求得b的取值范围;
(2)根据直线y=x+b易求得OB=OC,即可得出∠OCB=45°,根据轴对称的性质易求得∠ACD=45°.即可求得∠ACO=90°,从而求得C的纵坐标为-3,得出C的坐标为(0,-3),即可求得直线y=x-3,然后联立方程求得交点D的坐标,根据三角形面积公式即可求得△OBD的面积.
解:(1)当点D和点O重合时,
将点![]() 代人
代人![]() 中,得
中,得![]() ;
;
当点D和点A重合时,将点![]() 代入
代入![]() 中,
中,
得![]() ,即
,即![]() ,
,
![]() 的取值范围是
的取值范围是![]() .
.
(2)将点![]() 代入
代入![]() 中,得
中,得![]() ,即
,即![]()
![]() 直线OA的解析式为
直线OA的解析式为![]() .
.
在![]() 中,令
中,令![]() ,则
,则![]() ,
,
![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() ,
,
![]()
![]() ,
,
又![]()
![]() .
.
![]() 点A关于直线BC的对称点
点A关于直线BC的对称点![]() 恰好落在y轴上,
恰好落在y轴上,
![]() 垂直平分
垂直平分![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
即![]() .将点
.将点![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]()
![]() 直线BC的解析式为
直线BC的解析式为![]() .
.
由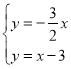 ,得
,得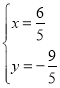 ,
,
![]() 点
点![]() .
.
![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)在函数![]() 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.