题目内容
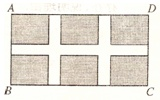
 某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.设人行道的宽为x米,则x=
某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.设人行道的宽为x米,则x=
- A.1
- B.2
- C.2或36
- D.1或2
B
分析:六块草坪组合到一起,正好构成一个矩形,根据这矩形的面积,设人行道的宽为x米,则矩形的长是(36-2x)m,宽是(20-x)m,即可得到方程(36-2x)(20-x)=96×6;
解答:设人行道路的宽为x米,根据题意得:
(36-2x)(20-x)=96×6;
解得:x=2或x=36(舍去)
故选B.
点评:本题考查了一元二次方程的应用,此类题是看准题型列出方程,题目不难,重在看准题;每一块草坪的面积=草坪的长×草坪的宽.
分析:六块草坪组合到一起,正好构成一个矩形,根据这矩形的面积,设人行道的宽为x米,则矩形的长是(36-2x)m,宽是(20-x)m,即可得到方程(36-2x)(20-x)=96×6;
解答:设人行道路的宽为x米,根据题意得:
(36-2x)(20-x)=96×6;
解得:x=2或x=36(舍去)
故选B.
点评:本题考查了一元二次方程的应用,此类题是看准题型列出方程,题目不难,重在看准题;每一块草坪的面积=草坪的长×草坪的宽.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.设人行道的宽为x米,则x=( )
某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.设人行道的宽为x米,则x=( )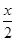 )=
)= ×96×6,其中正确的个数为( )
×96×6,其中正确的个数为( )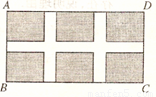

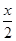 )=
)= ×96×6,其中正确的个数为( )
×96×6,其中正确的个数为( ) )=
)= ×96×6
×96×6