题目内容
●探究
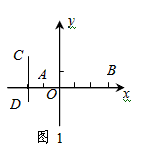
(1)在图1中,已知线段AB,CD,其中点分别为E,F。
①若A(-1,0),B(3,0),则E点坐标为__________;
②若C(-2,2),D(-2,-1),则F点坐标为__________;
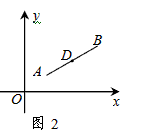
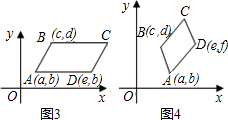
(2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程;
●归纳
无论线段AB处于直角坐标系中的哪个位置,
当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y) 时,x=_________,y=___________;(不必证明)
●运用
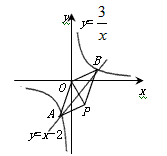
在图2中,一次函数y=x-2与反比例函数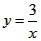 的图象交点为A,B。
的图象交点为A,B。
①求出交点A,B的坐标;
②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标。
(1)在图1中,已知线段AB,CD,其中点分别为E,F。
①若A(-1,0),B(3,0),则E点坐标为__________;
②若C(-2,2),D(-2,-1),则F点坐标为__________;
(2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程;
●归纳
无论线段AB处于直角坐标系中的哪个位置,
当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y) 时,x=_________,y=___________;(不必证明)
●运用
在图2中,一次函数y=x-2与反比例函数
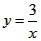 的图象交点为A,B。
的图象交点为A,B。①求出交点A,B的坐标;
②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标。

解: 探究:(1)①(1,0);②(-2, ); ); |
|
(2)过点A,D,B三点分别作x轴的垂线,垂足分别为A′,D′,B′,则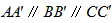 , ,∵D为AB中点,由平行线分线段成比例定理得, 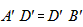 ∴OD′ 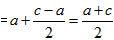 , , , ,同理可得D点的纵坐标是 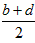 , ,∴AB中点D的坐标为( 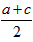 , ,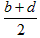 ); ); |
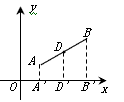 |
归纳: , , , , |
|
运用:①由题意得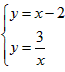 解得 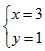 或 或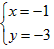 , ,∴即交点的坐标为A(-1,-3),B(3,1), ②以AB为对角线时,由上面的结论知AB中点M的坐标为(1,-1), ∵平行四边形对角线互相平分, ∴OM=OP,即M为OP的中点, ∴P点坐标为(2,-2), 同理可得分别以OA,OB为对角线时,点P坐标分别为(4,4) ,(-4,-4), ∴满足条件的点P有三个,坐标分别是(2,-2) ,(4,4) ,(-4,-4)。 |
 |

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目


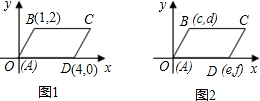
 时,
时,
 ,所以S△DBE=x
,所以S△DBE=x